Урок "ъгъл между права"

урок декодиране Текст:

Ъгълът между правите

Ние вече разгледани три случая на взаимно пряк място:

- права, които имат само една обща точка, т.е. линии се пресичат

- линии не се пресичат, но се намират в една и съща равнина; линии са успоредни

- линии не се намират в една равнина, т.е. пресечените линии

Ъгълът между пресичащи се линии по-долу ъгъл, който е не по-голяма от всеки от другите три ъгли (т.е., най-малкият от четирите ъгъла, образуван).

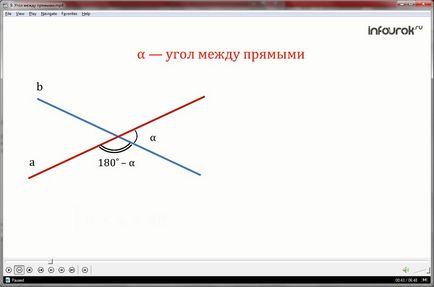
Ако линиите са перпендикулярни, стойността на ъгъла между пресичащи се линии ще бъде равна на 90.

Следователно, ъгълът между пресичащи се линии може да бъде остра или права, и величина е по-голяма от 0, но по-малко от или равно на 90

Разгледахме ъглите между пресичащи се линии в една и съща равнина. Опитайте се да определите ъгъла между кос линии.

За да направите това, ние ще изградим прави линии, успоредни на данните, така че те се намират в една и съща равнина. (Снимка)

Така за кос линии АВ и CD ъгъл е A₁K₁D₁ ъгъл, образуван от пресичането прави линии и A₁V₁ S₁D₁ паралелно АВ и CD съответно.

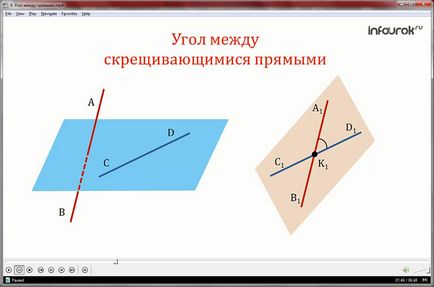
Определете дали A1K1D1 стойност зависи от избраната точка K₁ на.

Забележка произволна точка K₂ и да го направи чрез пряка и A₂B₂ C₂D₂ успоредно на AB и CD, съответно.

На една от линиите, например, CD-та да вземе точка К "и изграждане на A'B", съдържащ даден момент.

Според теоремата на три успоредни линии, A₁B₁ || A₂B₂ || A'B ", тъй като всеки един от тях е успоредна на AB.

От теоремата на три успоредни линии C₁D₁ || C₂D₂.

Следователно A'K'D странични ъгли, A₁K₁D₁ A₂K₂D₂ съответно и съща посока.

Така че, A'K'D = A₁K₁D₁ = A₂K₂D₂ от теоремата на ъглите с codirectional страни.

По този начин, след като е обсъдил няколко различни конструкции по отношение на пунктовете K₁, K₂, K "Стигнахме до извода, че:". Големината на кос ъгъл между прави линии от точката за избор е независим "

Ние считаме, че стойността на ъгъла между кос линии.

Пред нас AB и CD - кос линии, AB и - застъпване, както и за и CD - паралелно.

Какво е ъгълът между линии АВ и CD, ако:

Тъй AOF = 49˚; НА || CD, на кос ъгъл между редовете АВ и CD е 49˚.

б) Ако VOF = 104˚. ъгълът между правите линии АВ и CD е 76˚. Тъй като ъгълът между пресичащи се линии и AB НА вече 0˚, но по-малко от или равно на 90˚ и следователно равен на AOF = 180˚ - 104˚ = 76˚ собственост на съседните ъгли.

Ако AOF = 151˚. ъгълът между правите линии АВ и CD е 29˚.

По дефиниция, ъгълът между правите, че не трябва да надвишава 90 °, а ъгълът между пресичащи се линии на и AB е 180˚ - 151˚ = 29˚, откъдето идва и кос ъгъл между редовете AB и CD е 29˚.

ACD правоъгълен триъгълник с прав ъгъл и С е равнобедрен триъгълник ABC с AC база лежат в различни равнини. Точка F, К, М и М са средите на страните AB, BC, CD и DA съответно. ABC = 28˚, MN = ND = 3 cm.

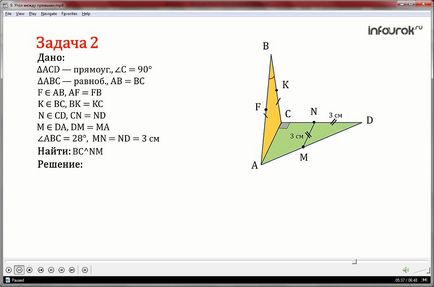
Определяне на ъгъла между редовете преди Христа и Ню Мексико, АД и ФК.

Нека помним, че ако отсечката, свързваща средата на двете страни на триъгълника, той е средната линия,

И теоремата на средната линия на триъгълника е равна на половината от трета страна, и успоредно с него.

Директен AC и MN са успоредни, като MN средната линия на триъгълника ACD.

Тогава се на ъгъла между BC и Ню Мексико е равен на ъгъла между АС и НЧ, и равен на БМА на ъгъл.

Помислете триъгълник ABC при условие, че е равнобедрен и AC основата му, тук имаме БМА ъгли и вие сте на ъглите в основата на равнобедрен триъгълник,

От теоремата за сбор от ъглите на БМА триъгълник ъгъл изрази тя е равна на половината от разликата на 180 градуса и ъгъл ABC.

Заместването на стойността на ъгъла ABC, ВСА намери ъгълът е 76 градуса

Ъгълът между редовете BC и MN е равен на 76 градуса.