Прекрасна граница - това

Обърнете внимание на едностранни граници и, и да докаже, че те са равни на 1.

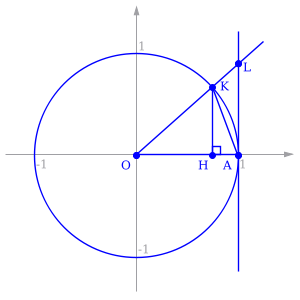
Да. Отлагане този ъгъл на единица кръг (R = 1).

К точка - точката на пресичане на лъча с кръг, и точка L - с допирателната към единичната окръжност в точка (1, 0). К прожекционни точки на оста вола - H точка.

Замествайки в (1), получаваме:

Умножена по sinx:

Нека да мине до границата:

Намери левостранна граница:

а има и леви и десни едностранни ограничения 1 и поради това ограничение е самата 1.

Вторият забележителен граница

Доказателство втори забележителна граница:

Доказателство втори забележителен граница за случая на последователност (т.е., положителни стойности за х)

Ние първо да докаже теоремата за последователността

От това уравнение (1) следва, че с увеличаване на п редица положителни отношение на страничните увеличава дясно. Освен това, чрез увеличаване на броя п ubyvet следователно увеличаване величина. Следователно, последователността - се увеличава. докато

Ние показваме, че той е ограничен. Замяна на всяка скоба от дясната страна по един, от дясната страна ще се увеличи, ние получаваме неравенството

Засилване на получената неравенството, замени 3,4,5, ... заставане в знаменателя на броя на фракция 2:

Сума в скоби се намери формула размера на експоненциално членове:

Така, последователността е ограничена по-горе, при следните неравенства (2) и (3).

Поради това, на базата на теоремата на Вайерщрас (последователност критерий конвергенция) последователност е монотонно увеличаване и ограничения лимит средства е представена от буквата Е. Т.е.

Знаейки, че вторият забележителен граница за истинските положителни стойности х, се окаже вторият забележителен лимит за недвижими х, т.е. Ние доказваме, че. Ние считаме, че два случая:

1. Да. Всяка стойност на х е между два положителни числа, където п = [х] - е цялата част на х.

От това следва, че така. Ако и след това. Поради това, в зависимост от срока, ние имаме. Въз основа на (функция на междинно съединение граница) съществуването на граници.

2. Нека. Ние се заместването - х = Т. след това

От тези два случая предполага, че за всяко х.

Последици от втората забележителна граница:

Забележително логаритмична граница

Забележително индикативна гранична

Забележително ограничение по мощност

забележителен не е пределът.
Една добра граница - границата на мъртвите.

Вижте какво "Wonderful граница" в други речници:

д (номер) - Този термин, има и други приложения, вижте Е. Да не се бърка с броя на тип Ойлер аз .. Да не се бърка с постоянен Ойлер. Ирационално номера γ ζ (3) √2 √3 √5 φ α д π δ ... Wikipedia

Разкриване на несигурност - методи на неопределеността за оповестяване за изчисляване на сроковете на функции, определени от формули, които водят до формална смяна в тези екстремни стойности на аргумента, са безсмислени, че се превръща в изрази като: ... ... Wikipedia

Неопределеността граници - оповестяване методи несигурност на изчисляването на границите на функции, определени формули, които водят до заместване в тези гранични стойности официално аргумент са безсмислени, т.е. трансформирани в тип експресия. 0/0, 00 ... Wikipedia

Несигурност (математика) - оповестяване методи несигурност на изчисляването на границите на функции, определени формули, които водят до заместване в тези гранични стойности официално аргумент са безсмислени, т.е. трансформирани в тип експресия. 0/0, 00 ... Wikipedia

Оповестяване несигурност - оповестяване методи несигурност на изчисляването на границите на функции, определени формули, които водят до заместване в тези гранични стойности официално аргумент са безсмислени, т.е. трансформирани в тип експресия. 0/0, 00 ... Wikipedia

E (математическа константа) - д математическа константа, основата на натуралната логаритмична, а трансценденталната ирационално число. Понякога номер д нарича броят на Ойлер (да не се бърка с т. Н. Някак Ойлер номера) или номер на Напиер. Обозначен с малки букви "е". ... ... Wikipedia

Neperovo брой - д математическа константа, в основата на натуралния логаритъм, класи ирационални номер. Понякога номер д нарича броят на Ойлер (да не се бърка с т. Н. Някак Ойлер номера) или номер на Напиер. Обозначен с малки букви "е". ... ... Wikipedia

Предишен ◈ Следващото