Как да намерите част на успоредник
препис
1 Виж успоредник страна на свойствата успоредника: 1. противоположните страни са успоредни и противоположни ъгли са равни на 2. 3. пресечната точка на диагоналите, ги разделя формула половина странични дължини чрез диагонала и на ъгъла между тях. α, β - ъгълът между диагонали Формула страни на успоредник чрез диагонала и ъгъла между тях (с косинусова теорема), (а, б):
Формула 2 през страните на успоредник и диагонална посока, (А, В): Формула страни на успоредник, (а, б): Формула дължини на страните на успоредник чрез височина.
3 Н б - височината на страничната б Н А - височината на страната на α, β - краища на страните на успоредник формула на успоредник чрез височината на, (а, б): По-интересно формула успоредник: α - остър ъгъл между диагонали формула сума от квадратите на диагоналите:
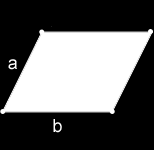
Формула 4 квадрат разлики страни: Как да намерите диагонал на успоредник свойства успоредника: 1. противоположните страни са успоредни и противоположни ъгли са равни на 2. 3. пресечната точка на диагоналите, ги разделя наполовина дължината на диагонала на успоредник през стените, диагонал и известен ъгъл. α, β - Формула успоредник ъгли диагонално страните и ъглите на успоредник (в косинус), (Г, г):
Формула 5 диагонално през стените и диагонал честота (от екв размер диагонали на квадрати), (D, D): дължината на диагонала на успоредник през зона известна и диагонален ъгъл. α, β - ъгълът между диагонали
6 S - площ на успоредник формула диагоналната в квадрата и диагонала на известен ъгъл между диагонали, (D, D) на сумата от квадратите на диагоналите на Формула сумата на успоредник от квадратите на разлика на площади и диагоналите на страните успоредника: а - остър ъгъл между диагоналните сумите на диагоналите на квадрата формула. Намерете най-острият ъгъл на ъгъла на успоредник на свойствата на успоредник:
7 1. 2. противоположни ъгли са равни косинусна тъп ъгъл, винаги има отрицателна стойност: COS β <0 α - острый угол β - тупой угол Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов): Формула синуса острого и тупого углов через площадь (S) и стороны: Формулы соотношения острого и тупого углов:
8 за определяне на ъгъла в градуси или радиани или употреба funktsiiarccos arcsin формула квадрат разлики страни: Виж ъгълът между диагоналите на свойствата успоредника ъгли между диагоналите на успоредник: 1. 2. противоположни ъгли са равни косинусна тъп ъгъл, винаги има отрицателна стойност: COS β <0
9 α - остър ъгъл между диагонали р - тъп ъгъл между диагоналите на Формула косинус остри и тъпи ъгли между диагоналите през стените и диагонал (на косинус теорема): Формула задължително остри и тъпи ъгли през повърхността (S) и диагоналите:
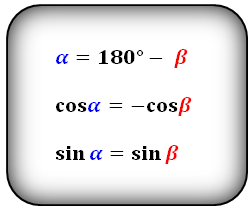
10 Формула връзка остри и тъпи ъгли между диагоналите: За определяне на ъгъла в градуси или радиани, използвайте функцията arccosi arcsin дължина и свойства на ъглополовящата на свойствата успоредника ъглополовяща успоредник - ъглополовяща по дефиниция разделя ъгълът половината - разполовяване порязвания равнобедрен триъгълник (в този случай триъгълници ABF и ДКЦ) - ъглополовящи съседните ъгли се пресичат под прав ъгъл (90) - ъглополовящи на противоположните ъгли са равни и успоредни
11 AF - ъглополовяща на остър ъгъл DK - ъглополовяща на тъп ъгъл а - остър ъгъл Р - тъп ъгъл - долната страна б - големи странични така като триъгълници ABF и ДКЦ, равнобедрен следователно валиден идентичност: Дължина ъглополовяща успоредник L - ъглополовяща паралелограм на , б - страничен
12 α, β - ъгли дължина формула ъглополовяща чрез страна и ъглите, (L): Виж височината на успоредник и ъгъл между тях височина - перпендикулярна произход от върха на ъгъла на противоположната страна Н Б - височината на страничната б Н А - височината на страната на α , β - успоредник ъгли формула дължина височина на успоредник чрез страна и ъгълът, (Н в, Н а):
13 остър ъгъл на пресичане височини равни на остър ъгъл на успоредник. Тъп ъгъл на пресичане височина равна тъп ъгъл успоредник.