Ъгълът между редовете - studopediya
Ъгълът между правите линии в пространството ще се нарича от всички съседни ъгли, образувани от две линии, изготвени чрез паралелни данни на произволна точка.
В пространството дадени две линии:
Очевидно е, че на ъгъла # 966; между редовете може да ъгъла между посоката вектори и. Тъй като. формула на косинуса на ъгъла между векторите получат
.
Условия паралелни и перпендикулярни на две прави линии са еквивалентни на условията на паралелно и перпендикулярно на посоката вектори и:
Две линии са успоредни, ако и само ако техните съответни коефициенти са пропорционални, т.е. L1 L2 паралелно единствено и само ако паралел.
Две линии са перпендикулярни, ако и само ако сумата от произведенията на съответните коефициенти равни на нула :.
Ъгълът между правата линия и равнината
Нека ред г - не е перпендикулярна на плоскостта # 952 ;;
г '- проекцията върху равнина линия г # 952 ;;
Най-малкият от ъглите между редовете г и г ', което наричаме ъгълът между линията и равнината.
Ние го обозначи като # 966 = (г, # 952)
Ако г ⊥ # 952;. след това (г, # 952) = π / 2
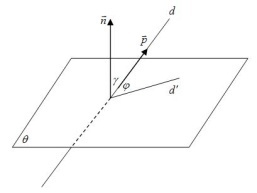
Oi → → й к → - правоъгълна координатна система.
Уравнението на равнината:
Ние вярваме, че линия зададената точка и вектор посока: г [М 0, р →]
Векторът п → (А, В, С) ⊥ # 952;
След това остава да се определи ъгълът между векторите п и р → →, ние го означават като # 947 = (п →, стр →).
Ако ъгълът # 947;<π/2. то искомый угол φ=π/2−γ .
Ако ъгълът # 947;> π / 2. след това желания ъгъл # 966 = # 947; -π / 2
След това ъгълът между правата линия и равнината може да се приеме от формулата:
Vopros29.Ponyatie квадратното форма. Sign-определеност на квадратните форми.
Квадратичен форма й (x1. X2. ... хп) п недвижими променливи x1. x2. ... хп е сумата от формата
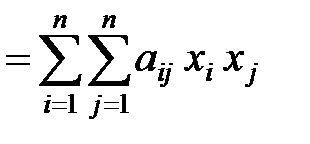
където Aij - някои цифри, наречена коефициенти. Без ограничение на общността можем да предположим, че Aij = Aji.
Квадратичната форма се нарича валидно, ако Aij Î GR. Матрицата на квадратна форма е матрица, съставена от неговите коефициенти. Квадратичен форма (1) съответства на уникален симетрична матрица
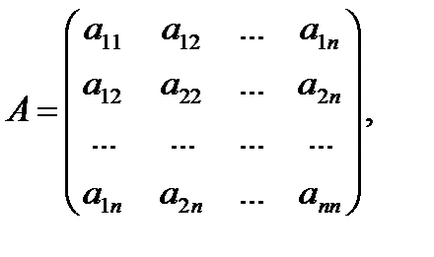
Обратно, всяка симетрична матрица (2) съответства на квадратна форма само до означават променливи.
Рангът на квадратното форма се нарича ранг на матрицата си. В квадратна форма, наречена nondegenerate ако е неособена матрица матрица А (припомни, че матрицата е неособена матрица, ако неговото детерминанта е нула). В противен случай квадратното форма е дегенерат.
В квадратна форма (1) е положително определено (или силно положителен), ако
А е положително определена квадратна форма й (х) е също така казва, че е положителен определен. Следователно положителен определена квадратна форма съответства само положителен определена матрица и обратно.
В квадратна форма (1) е решена отрицателен (или строго отрицателна) ако
По същия начин както по-горе, отрицателна определен матрични четворни-квадратичен форми също наречени отрицателен определен.
Следователно, с положителен (отрицателен), определена Quadra-Ung форма на J (х) достига минимум (максимум) стойностите й (х) = 0 за х = (0, 0, ..., 0).
Имайте предвид, че повечето от квадратните форми не е сигурен признак, че е, че те не са нито положителни, нито отрицателни. Такива квадратните форми се отнасят до 0, а не само в началото, но и в други места.
Когато N> 2, изисква специални критерии за валидиране вход определеност на квадратните форми. Нека ги разгледаме.
Основни непълнолетни лица на квадратното форма се нарича малка:
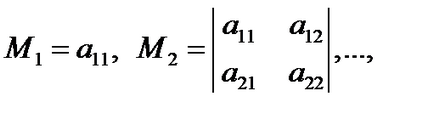
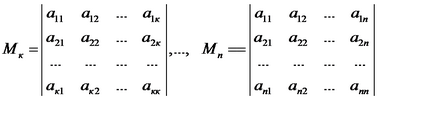
това означава, че е малолетни и непълнолетни лица, за 1, 2, ..., N на матрица А. намира в горния ляв ъгъл, последното от които съвпада с детерминантата на матрицата А.
Критерий положителен определеност (критерий Sylvester)
За квадратна форма й (х) = х Т Ах е положително определена, че е необходимо и достатъчно всички основни непълнолетни на матрицата А са положителни, което е: M1> 0, M2> 0, ..., Mn> 0. Критерий за отрицателен сигурност за квадратна форма J (х) = х Т Ах е отрицателно определя, че е необходимо и достатъчно неговите основни непълнолетни са положителни дори ред и нечетен - отрицателно, т.е. M1 .. <0, M2> 0, М3 <0, …, (–1) n