Геометрията на равнината (планиметрия)

Правилен шестоъгълник - изпъкнал шестоъгълник, всички, чиито ъгли са равни и всички страни са равни.

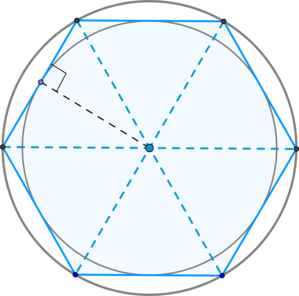
\ (\ Blacktriangleright \) Всеки ъгъл на правилния шестоъгълник е \ (120 ^ \ циркулационната \).

\ (\ Blacktriangleright \) Някои от правилния шестоъгълник може да бъде описан като кръг: радиус е равен на една страна.

\ (\ Blacktriangleright \) Голям диагонал на правилен шестоъгълник го разделете на \ (6 \) равностранен триъгълник, чиято височина е равна на радиуса на вписан кръг в правилен шестоъгълник.

\ (\ Blacktriangleright \) центрове вписан и окръжности около правилния шестоъгълник е пресечната точка на диагоналите на големия шестоъгълник.

\ (\ Blacktriangleright \) Площта на правилен шестоъгълник с страна \ (а \) е равна на \ [S = \ dfrac2a ^ 2 \]

задача 1 <ЕГЭ

Радиусът на кръга е вписан правилен шестоъгълник \ (\ SQRT \). Пътувайте, този радиус на окръжността на шестоъгълника.

Чрез имот редовен радиус шестоъгълник \ (R \) на вписан кръг е перпендикуляра съставен от центъра на правилен шестоъгълник (центъра на вписан и описаните окръжности) на страната на шестоъгълника; и това перпендикулярно попада в средата на страната.

Също така, от имуществото на правилен шестоъгълник окръжност радиус кръга е равен на една страна \ (а \). След това, от правоъгълен триъгълник:

\ [A ^ 2 = \ наляво (\ Frac а2 \ дясно) ^ 2 + R ^ 2 \ четири \ стрелкаНадясно \ четири а = \ dfrac 2 \, г \ четири \ стрелкаНадясно \ четири а = \ dfrac2 \ cdot \ SQRT = 4 \]

По този начин, радиусът на кръга е равен на \ (4 \).

задача 2 <ЕГЭ

Намерете разстоянието между две успоредни страни на правилен шестоъгълник със страна \ (\ SQRT \).

Помислете за правилен шестоъгълник \ (ABCDFE \) и в него триъгълник \ (ABC \). Двойка успоредни страни са \ (AB \) и \ (DF \). \ (BC \) и \ (FE \). \ (CD \) и \ (EA \).
Не забравяйте, че ъгълът на правилен шестоъгълник е равна на \ (120 ^ \ циркулационната \).

\ (\ триъгълник ABC \) равнобедрен (\ (AB = пр \, \)), следователно, \ (\ ъгъл BAC = 0,5 \ cdot (180 ^ \ Circ-120 ^ \ Circ) = 30 ^ \ Circ \ ). По този начин, \ (\ ъгъл CAE = 120 ^ \ Circ-30 ^ \ Circ = 90 ^ \ Circ \).

Следователно \ (AC \) - разстоянието между страните \ (AE \) и \ (CD \) (за определяне на разстоянието между две успоредни линии - сегмент, съставен от всяка точка на една права линия, перпендикулярна на втория ред).

Намираме \ (AC \) от правилото за косинус (\ (AB = BC = а = \ SQRT \)):

\ (AC ^ 2 2 = а + ^ а ^ 2-2a ^ 2 \ cdot \ cos120 ^ \ Circ = \ cos120 ^ \ 2а ^ 2 (1 Circ) = 2 \ cdot 108 \ cdot \ наляво (1+ \ frac12 \ вдясно) = 3 \ cdot 108 \ четириядрен \ стрелкаНадясно \)

Дейност 3 <ЕГЭ

Площта на правилен шестоъгълник е равна на \ (24 \ sqrt3 \). Да се ​​намери дължината на по-голямата си диагонал.

Чрез собственост на правилен шестоъгълник голям диагонал му два пъти ръката му. Следователно, ако \ (AB = а \). на \ (AD = BF = CE = 2а \).

защото Това диагонал правилен шестоъгълник разделена на 6 равностранни триъгълници, площта на всеки е равен на \ (\ frac4 на ^ 2 \). общата площ на шестоъгълника е равно на

\ [S = 6 \ cdot \ dfrac4a ^ 2 = 24 \ sqrt3 \ четири \ стрелкаНадясно \ четири а = 4 \ четири \ стрелкаНадясно \ четири AD = 2а = 8. \]

задача 4 <ЕГЭ

За кръг окръжност около правилен шестоъгълник \ (ABCDEF \). в точка \ (A \) проведе тангента. Намерете ъгълът между тази тангента и направо \ (AD \). Отговор даде градуса.

защото да бъде в центъра на правилен шестоъгълник около кръга е пресечната точка на диагоналите на голям, той се намира на сегмент \ (AD \) на. т.е. \ (AD \) - диаметърът на описаните окръжности. защото радиус насочено към точката на контакт, перпендикулярно на допирателната, ъгълът между допирателната и \ (AD \) е равна на \ (90 ^ \ Circ \).

задача 5 <ЕГЭ

За правилен шестоъгълник \ (ABCDEF \) описва окръжност с център в точка \ (О \). Колко пъти площта на шестоъгълника по-голяма площ на триъгълник \ (AOK \). където \ (K \) - от страна на средната \ (BC \).

Чрез собственост на правилен шестоъгълник окръжност лежи в пресечната точка на диагоналите големи. Следователно \ (AO \) - радиусът на кръга. Също така, от собственост на радиуса на кръга е страна на правилния шестоъгълник, по този начин, \ (AB = AO = х \).

защото \ (\ Триъгълник АОВ \) - е правилна, \ (\ ъгъл АОВ = 60 ^ \ Circ \). \ (\ Триъгълник BOC \) също е вярна. защото от състоянието \ (OK \) - медианата в правото \ (\ триъгълник BOC \). тя и ъглополовяща, това е, \ (\ ъгъл BOK = \ frac12 \ cdot 60 ^ \ циркулационната = 30 ^ \ циркулационната \). По този начин, \ (\ ъгъл AOK = 90 ^ \ Circ \). тоест, \ (\ триъгълник AOK \) - правоъгълна.

Следователно \ [S _ = \ dfrac12 \ cdot AO \ cdot OK = \ dfrac х2 \ cdot OK \]

Площта на правилен шестоъгълник е равна на сумата от площите на шест равни триъгълници:

\ [S_ = 6 \ cdot \ dfrac12 \ cdot пр \ cdot OK = 6 \ cdot \ dfrac х2 \ cdot OK \]

задача 6 <ЕГЭ

За правилен шестоъгълник \ (ABCDEF \) описва окръжност с център в точка \ (О \). Можете да намерите голям страни на триъгълник \ (AOK \). където \ (K \) - средната точка на странична \ (BC = \ sqrt7 \) шестоъгълник \ (ABCDEF \).

Чрез собственост на правилен шестоъгълник окръжност лежи в пресечната точка на диагоналите големи. Следователно \ (AO \) - радиусът на кръга. Също така, от имуществото на радиуса на кръга е на страната на правилния шестоъгълник, като по този начин, \ (AB = AO = \ sqrt7 \).

защото \ (\ Триъгълник АОВ \) - е правилна, \ (\ ъгъл АОВ = 60 ^ \ Circ \). \ (\ Триъгълник BOC \) също е вярна. защото от състоянието \ (OK \) - медианата в правото \ (\ триъгълник BOC \). тя и ъглополовяща, това е, \ (\ ъгъл BOK = \ frac12 \ cdot 60 ^ \ циркулационната = 30 ^ \ циркулационната \). По този начин, \ (\ ъгъл AOK = 90 ^ \ Circ \). тоест, \ (\ триъгълник AOK \) - правоъгълна.

Следователно, голяма партия в \ (\ триъгълник AOK \) - е хипотенуза \ (AK \). Според питагорова теорема на \ (\ триъгълник BOK \) (\ (OK \) също е в разгара си):

По този начин, Питагор на \ (\ триъгълник AOK \) от Теорема:

задача 7 <ЕГЭ

За правилен шестоъгълник \ (ABCDEF \) описва окръжност с център в точка \ (О \). Разстоянието от точка \ (О \) на един от своите страни е равна на \ (4 \ SQRT \). Намерете радиуса на този кръг.

Радиусът на кръга около правилния шестоъгълник е на страната на шестоъгълника.

\ (OK \) - височината на триъгълник \ (AOF \). понижава от \ (О \). Тъй като разстоянието от точка, за да линия - дължина на перпендикулярно спадна от този момент нататък тази линия, а след това \ (OK = 4 \ SQRT \).
Нека \ (R \) - радиусът на кръга, докато \ (OF = R \). \ (KF = 0,5R \) (от \ (OK \) Повече и медиана), като по този начин Питагоровата \ (R ^ 2 = (0,5R) ^ 2 + (4 \ SQRT) ^ 2 \ ). където \ (R = 8 \).

На "правилен шестоъгълник и неговите свойства" в изпита по математика е традиционно възложени няколко задачи. Нещо повече, в зависимост от състоянието на ученика може да се наложи като подробен и кратък отговор. Ето защо в хода на подготовката за доставка на завършилите тестови квалификация определено трябва да се научите как да решават проблеми в използването на свойствата на тази цифра, в който трябва да намери своя страна, диагонал, радиус на кръг с вписан правилен шестоъгълник, и така нататък. Г.

За да се запълни пропуските в знанията, "помпа" умения и подобряване на собствените си знания по този въпрос ще помогне на образователната проекта "Shkolkovo". Нашите експерти са изготвени и представени на цялата материална база, за да се подготвите за изпита по възможно най-достъпна форма.

За да затвърдят знанията, ние предлагаме да практикуват в съответните им роли. За да ги намерите, ще бъде в състояние да "каталога" раздел. За всяко упражнение, сайтът представи алгоритъм за решаване и верния отговор.

За да се подготви за изпита студентите от Москва и други градове са онлайн. всяко упражнение може да се спаси в случай на нужда в раздела "Любими". В бъдеще, тази задача може да бъдат преразгледани и, например, да се обсъждат на алгоритъма на своите решения с преподавателя.

С кликването върху "Регистриране" Приемам условията на Споразумението за потребителя