Знаеш ли какво е рационално и какво числа се нарича рационално

В далечното минало, когато има е изобретен смятане система, всички хора, броят на пръсти. С появата на аритметиката и основни математика то е станало много по-лесно и по-практично да водят регистри на стоки, продукти и предмети от бита. Въпреки това, тя изглежда като модерна система за изчисление: какви видове се разделят на броя на наличните, а това означава "един рационален вид числа?" Нека си го кажем.

Колко вида на номера, съществува по математика?

Самата понятието "номер" се отнася до определена единица на всеки обект, който се характеризира количествените сравнителни или редни показатели. За да може правилно изчисляване на броя на конкретни елементи или извършване на математически операции с числа (сгънати размножават и др.), На първо място трябва да сте запознати с тези видове за числата.

1. Natural - това са цифрите разчитаме броя на обектите (..-малко положително число, равно на 1, логично е, че броят на естествените числа е безкраен, т.е., не е най-голямото естествено число). Комплект от естествени числа обикновено се означава с буквата N.
2. Числа. За този комплект включва всички естествени числа, докато тя прибавя към отрицателни стойности, включително броя "нула". Определяне на набор от числа се записва като латинската буква Z.
3. Рационални числа - тези, които психически можем да се превърнат в една малка част, в числителя на която ще принадлежат към набора от цели числа, а знаменателят - естествено. Точно под обсъждаме по-подробно какво означава да "рационално число", и даде няколко примера.
4. Реални числа - комплект, който включва всички рационални и ирационални числа. Този комплект е означена с буквата С.
5. Комплексни числа съдържат част от реална част и променлив брой. се използват при решаване на различни кубични уравнения, които на свой ред могат да бъдат във формулите по знак корен Комплексни числа е отрицателна експресия (I 2 = -1).

Какво искаш да кажеш "рационално": демонтаж примерите

Ако рационални числа са тези, които ние можем да представи под формата на обща фракция, се оказва, че всички положителни и отрицателни числа също са включени в комплекта на рационално. Всъщност, всяко цяло число, като 3 или 15, може да бъде представена като фракция където знаменател ще единица.

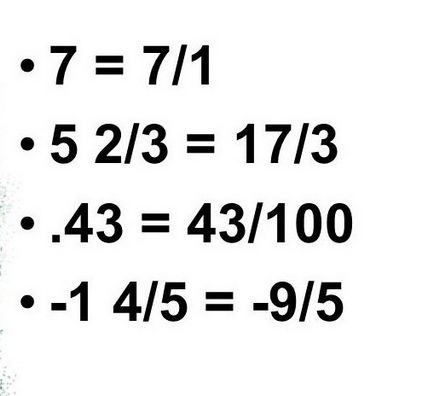
Фракции: -9/3; 7/5, 6/55 - са примери за рационални числа.

Какво означава "рационален израз"?

Продължавай. Вече обсъдихме какво означава да си рационален оглед на числата. Нека сега си представим математически израз, който се състои от сумата, разликата, продукт или различни частни цифри и променливи. Ето един пример: фракция, числителя на които е сумата на две или повече цели числа, и знаменателят включва цяло число, така и някои променлива. Той е този израз се нарича рационално. Въз основа на правилата "не може да се раздели на нула" можете да се досетите, че стойността на тази променлива не може да бъде такава, че стойността на знаменателя изчезва. Ето защо, при разглеждането на даден рационален израз, трябва първо да се определи обхватът на стойността на променливата. Например, ако знаменател от следния израз: х + 5-2, се оказва, че "X" не може да бъде равно -3. Наистина, в този случай, всички експресия става нула, обаче в разтвора трябва да бъде изтрита -3 число за дадена променлива.

Как да решим рационални уравнения?

Рационални изрази могат да съдържат доста голямо количество номера или дори две променливи, така че понякога решението им става трудно. За да се улесни разтвор на такава експресия се препоръчва за някои операции по рационален начин. И така, какво означава "рационално" и какви правила трябва да се прилагат в решението?

1. Първият тип, когато само трябва да се опрости израза. За тази операция може да се прибегне до намаляване на числителя и знаменателя на който не може да бъде принуден стойност. Например, ако има израз в числителя на 18x, 9x и знаменател, а след това, намаляване на двата показателя за 9x, получи число 2.
2. Вторият метод е практично, когато числителят имат мономен, а знаменателят - полином. Нека разгледаме един пример: в числителя има 5x, а знаменателят - 5x + 20x 2. В този случай, най-добре е да се направи променлива в знаменателя на скобите, ние получаваме следната форма на знаменателя: 5x (1 + 4x). А сега можете да използвате първото правило и опростяване на израза, намалявайки с 5 пъти повече в числителя и в знаменателя. Като резултат, ние получаваме малка част от формата 1/1 + 4х.

Какво мога да направя с рационални числа?

Наборът от рационални числа има редица функции. Много от тях са много сходни с характерен присъства в цели и естествени числа, се дължи на факта, че последният винаги е включена в комплекта на рационално. Ето някои свойства на рационални числа, знаейки, че можете лесно да реши всеки рационален израз.

1. Комутативност ви дава възможност да се измери два или повече номера, независимо от техния приоритет. Казано по-просто, за преместването на сума не се променя.
2. дистрибутивният имота ни позволява да се реши проблема с помощта на разпределителни закона.
3. На последно място, събиране и изваждане.

Дори учениците знаят какво означава "рационално оглед на номерата" и как да се решават проблеми на базата на такива изрази, така че възрастен човек образован просто трябва да си припомним поне основите на снимачната площадка на рационални числа.