В каноничен формата на втората крива за
Втори ред уравнение на формата
Той определя равнина крива. Една група от членове нарича квадратна форма, - линейна форма. Ако квадратна форма на квадратите съдържа само променливи, като цел се нарича канонични и ортонормирани базисни вектори, в които квадратна форма има каноничен форма, наречена главните оси на квадратна форма.
Матрицата се нарича матрицата на квадратна форма. Тук. За матрица, за да диагонал форма, с основа необходимо да се вземат собствените вектори на тази матрица, а след това, когато # 955; 1 и # 955; 2 - собствените стойности на B.
В основата на собствени вектори на квадратното форма В ще има каноничен вид.
Тази операция съответства на въртене на координатните оси. На следващо място, промяната на произхода, като по този начин да се отървем от линейната форма.
В каноничен формата на втората крива ред, където:
а) ако # 955; 1> 0; # 955; 2> 0 - елипса, по-специално, в # 955; 1 = # 955; 2 е кръг;
б) ако # 955; 1> 0, # 955; 2 <0 (λ1 <0, λ2>0) имаме хипербола;
в) ако # 955; 1 = 0 или # 955; 2 = 0, кривата е парабола и след осите на въртене на формата (тук # 955; 2 = 0). В допълнение към пълната квадрат, имаме :.
Пример. Като се има предвид уравнението на кривата
в координатна система (0, I, J), където.
1. Определете вида на крива.
2. За да донесе равенството на каноничната форма и се построи крива в оригиналната координатна система.
3. Намерете съответната координатна трансформация.
Решение. Тук е квадратна форма В = 3 х 2 + 10xy + 3Y 2 към основните оси, т.е., на каноничната форма. Матрицата на тази квадратна форма. Ние намерите собствени стойности и собствени на тази матрица:
Характерните уравнение:
; # 955; 1 = -2 # 955; 2 = 8. Квадратичен форма :.
Оригиналният уравнение определя хипербола.
Имайте предвид, че квадратното форма е двусмислен. Може ли да бъде написана, обаче, тип крива е останала същата - хипербола.
Дали основната ос на квадратното форма, което означава, собствени вектори на Б ..
Собствен вектор, съответстващ на броя # 955 = - 2, когато Х1 = 1 :.
Като единствен собствен вектор приемам вектор, където - дължината на вектора.
Координати втори собствен вектор, съответстващ на втората собствена стойност # 955; = 8, намираме от системата
.
; ,
Така че, ние имаме нова база ортонормален.
С (5) от параграф 4.3.3. преместите на нова основа:
или
Ние правим изрази на х и у в оригиналния уравнение и след преобразувания получаваме :.
Изберете перфектни площади. ,
Начертайте паралелни оси за превод в новото начало :.
Ако направите тези отношения в (*) и позволи на тези уравнения по отношение на x2 и y2. получаваме :. В тази координатна система, уравнението е от вида :.
За да се конструира крива на старата изграждането на нова система на координати: Х2 = 0 ос се дава с уравнението в стария координатна система X-Y-3 = 0 и Y 2 = 0 ос уравнение х + у-1 = 0. Като се започне нова координатна система 0 * (2, 1) е пресечната точка на тези прави линии.
За да се опрости възприемането разделя процеса в заговор за 2 етапа:
1. Преминаване към координатна система с х2 оси = 0, Y 2 = 0, уравнения, дадени в старото координатна система X-Y-3 = 0 и х + у-1 = 0, съответно.
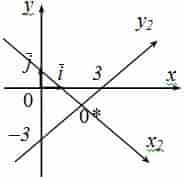
2. Изграждане на системата, получен в координатите на графиката.
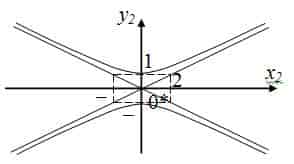
Окончателният вариант на графиката е както следва (виж как да се построи графика.):
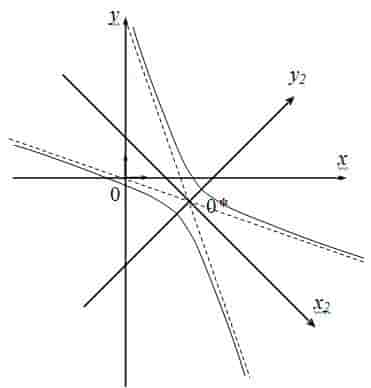
Задача. Доведе до канонична форма уравнение на линията 17x 2 + 12xy + 8у 2-20 = 0.
Пример 2 Решение: XML
Задача. Доведе до каноничната форма на уравнението от втори ред на линията, като се използва теорията на квадратичен форми и да се определи външния му вид. Уравнението на кривата на втория ред чрез екстрахиране на квадратен пълно редуцира до канонична форма. Решение: XML
Задача. Намаляване на уравнението на каноничната форма: 16x 2 - 9y 2 -64x - 8у 199 = 0.
Решение .Skachat решение: XML
Задача. За да се установи, че всеки от следното уравнение определя хиперболата и да намерите координатите на центъра С, полу-ексцентричност, уравненията на асимптоти и директорката на уравнението. Представят хиперболата на чертежите, посочени трикове, директорката и асимптотата.
Решение: Свали решение: XML
Задача. За да се установи, че всяка една от следните уравнения на елипса, и да намерят координатите на центъра С, полу-ексцентричност, директорка на уравнението. Изобразяват елипса в чертежа, посочване на оста на симетрия и фокусите на директриса.
Решение: Свали решение: XML