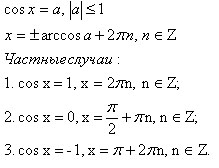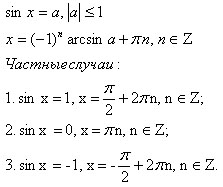Тригонометричните формула, превръщането на тригонометрични функции на формулата за двойно ъгъл

Съотношението между степента и ъгъла на радиана мерки

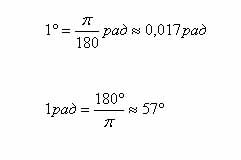
Определения:
Тригонометрични функции на остри ъгли могат да бъдат определени като отношението на дължините на страните на правоъгълен триъгълник.

Синус и косинус на ъгъла определя за всеки ъгъл α. На допирателната дефинирани за всички стойности на ъгъл а, с изключение на α = π / 2 + πn (а = 90 ° + 180 ° * п), п = 0, +/- 1, +/- 2 котангенс дефинирани за всички стойности на ъгъл а, α изключение = πn (α = 180 ° * п), п = 0, +/- 1, +/- 2.

Функция на греха α. защото α, сек α cosec α и има период на 2π и функциите и TG α CTG α - период π:

грях (a + 2πn) = грях α; cosec (α + 2πn) = cosec α;

COS (α + 2πn) = защото α; сек α + 2πn) = сек α;

TG (α + πn) = tgα;

CTG (α + πn) = CTG α; п = 0, +/- 1, +/- 2.

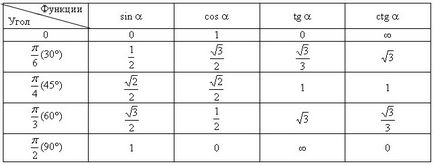
При изчисляването на стойностите на тригонометричните функции на всеки ъгъл се свежда до изчисляване на стойности на тригонометрични функции на остър ъгъл от следните правила:

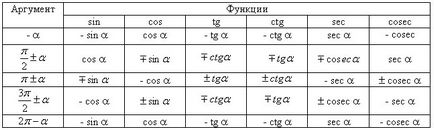
Някои от стойностите на тригонометричните функции

Основни тригонометрични идентичности

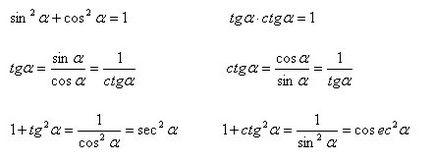
Дори или нечетни тригонометрични функции

(Х) функция F се нарича дори ако F (-x) = F (х).
(Х) функция F се нарича странно ако F (-x) = - F (х).
(Х) функция F се нарича или равна или нечетен във всички останали случаи.

грях α, TG алфа, CTG алфа и cosec алфа - нечетни функции.

грях (- а) = - SIN алфа TG (- α) = - TG α; CTG (- α) = - CTG α; cosec (- α) = - cosec α.

COS а и сек α - дори функция.

COS (- α) = защото α; сек (- α) = сек α.

Тригонометрични функции на сбор и разлика на ъгли

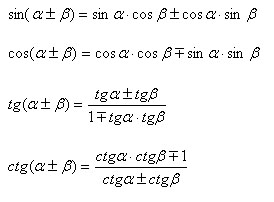
Експресия sinα, cosα, tgα чрез TG (α / 2)

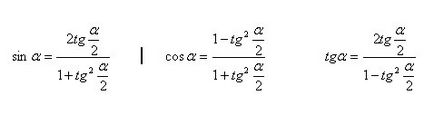
Експресията на някои тригонометрични функции чрез други

Тригонометрични функции на двойни, тройни и половина ъгли

знаци половин ъгъл формули в предните радикали се вземат в зависимост от знака на тригонометрични функции на лявата ръка.
Всяка една от формулите за тангенс и котангенс валидна само при условие, че всички негови функции ценности съществува.

Преобразуване сума (разлика) от тригонометрични функции работят (преобразуване на тригонометрични изрази във форма, удобна за логаритмуване).

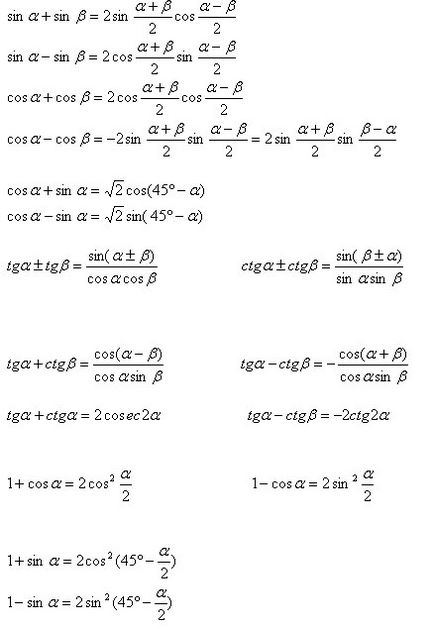
продукти за преобразуване на тригонометрични функции в сума.

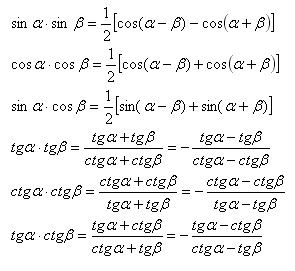
Дясната и лявата страна на всяка формула, която включва допирателната и (или) котангенс трябва да съществува едновременно.

Най-простият връзката между обратни тригонометрични функции.

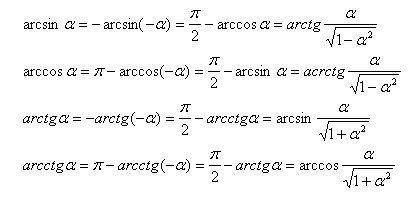
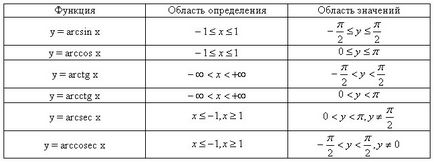
Решение на тригонометрични уравнения.