Срок софтуер хартия изпълнение на Алгоритъм на Дейкстра (изграждане на схеми за минимална дължина) -

Министерство на образованието и науката на Украйна

Kharkovsky Националния университет на Радиоелектроника

Тема: "Изпълнението на софтуер на Дейкстра алгоритъма (изграждане на схеми за минимална дължина)"

по дисциплина "Програмиране"

Студентските групи KI-05-4 Руденко DA

Петров О. В. Mashtalir SV

Забележка към обяснителния термин хартията: 23в. 5 фиг. Таблица 1. 5 секции, 3 приложения.

Предмет на изследване - графика с претеглят ръбове.

Целта на работата - разработване на програма за демонстрация за използване на Алгоритъм на Дейкстра.

метод на изследване - изучаване на литература, съставянето и отстраняване на грешки програма на компютър.

Можете да използвате тази програма, за да намерите най-късото разстояние между две точки.

Програмата е написана на C ++ в Microsoft Visual C ++ 6.0 среда. Ключови думи: Дейкстра, графики, вертикали, ръбове, тежести, път, тегло, етикети, програма тип, оператори, функции, контури, близост матрица.

Благодарение на широкото използване, теорията за намиране на най-кратките пътища са се развива интензивно.

Намирането на най-краткия път - е жизнено важно и се използва почти навсякъде, от намирането на оптималния маршрут между два обекта на земята (например, най-краткия път от вкъщи до университета), автопилот системи, за да откриете най-оптималния маршрут в областта на транспорта, превключване, информационен пакет, в интернет и т.н. п.

Най-краткият път се смята с помощта на математически обект, наречен графика.

Има три от най-ефективните алгоритъм за намиране на най-краткия път:

· Dijkstra алгоритъм (използван да се намери оптимален маршрут между две възли);

· Floyd алгоритъм (за намиране на оптимален път между всички двойки от върховете);

· Ian алгоритъм (за намиране на к оптимални маршрути между два върха).

Тези алгоритми са лесно се срещнаха с малък брой върхове в графиката. С увеличаване на броя на задачите си за търсене на най-краткия път е сложно. Тук идва на помощ на модерни технологии

Компютърни съоръжения и информационните технологии са се увеличили възможността за такъв метод на всеобхватно на живот и творчество, като моделиране на обекти, явления и процеси - като тези, които съществуват в природата, както и тези, които са създадени изкуствено от човека.

Броят на обектите е сложно увеличава и природен моделиране (модели на сгради) се превърна нерентабилни, нерентабилна. Ето защо, започват да учат приложна математика. Използването на математически модели - уравнения, неравенства, формули и други подобни, се нарича математическо моделиране за развитие и адаптиране, които са ефективни са необходими числени методи.

За реализиране на големия потенциал на математическо моделиране е невъзможно без мощни средства за автоматизация на изчисленията, които са компютри. Благодарение на появата на компютрите и развитие на информационните технологии са методите и средствата за компютърна симулация, която може да решим сложни практически проблеми, като например управлението на големи енергийни системи, създаване на надеждни прогнози за времето и моделиране на културите регионални и национални системи, дизайн на самолети, кораби и др. Н. Computer модел - се поставя в компютъра набор от инструменти, които прилагат концепцията за компютри.

За изпълнение на модела на компютъра, голямата стойност има научна насока като програмиране. Без него компютърът е просто набор от устройства, вериги, които не могат да бъдат полезни.

Големите програми, тъй като на неговата сложност често съдържат грешки, които могат да причинят материални щети, а понякога и да застрашат живота на хората (например, управление на aviapolotami). В резултат на борбата с проблема с кода на три нови програмни концепции са разработени:

а) обектно-ориентирано програмиране (OOP);

б) Unified Modeling Language (UML);

в) инструменти за разработка на специализиран софтуер;

От всички обектно-ориентиран C ++ е най-широко използваният език. И с негова помощ в този курс се разработва проект Алгоритъм на Дейкстра.

1 ДЕКЛАРАЦИЯ на проблема и обхвата на неговите

Основната цел на този курс проект е софтуер изпълнение на алгоритъма се намери най-краткия път между всеки два върха на графика.

Програмата трябва да работи, така че потребителят влезе в броя на върховете, а дължината на ръбовете на графиката, а след обработка на тези данни да се показват най-краткия път между две дадени възли и дължината му. Не трябва да има най-различни резултати от търсенето, програмата не дава грешки и работи правилно.

Тази програма може да бъде използвана в дискретна математика към изучаването на графики или като визуална помощ, показващ използването на Алгоритъм на Дейкстра на практика.

2 ТЕОРИЯ

2.1 Информация за графиките

Графика G (ris.2.1.1), определена от множеството от точки (върха) Х1, Х2. хп. (Означен с X) и множество от линии (ръбове) А1, А2. AM. (Което е означен с А) свързване на всички или някои от тези точки. Така графиката G е напълно определена (и маркирани) двойка (X, А). Ако краищата на набор фокус, който обикновено е показано със стрелката, след което те се наричат ​​дъги и Графа с тези ребра се нарича насочено графика.

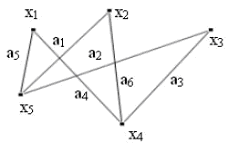
Например, ако на пътя не е два, еднопосочно движение и посоката на това движение е показано със стрелката.

Ако краищата не са ориентацията, графиката се ненасочена, (двупосочно движение).

насочена графика дъга означен подредени двойка, състояща се от начална и крайна върхове, неговата посока се приема, че се дава от първия връх на втория.

С (или ориентирани маршрут), насочени графика е последователност от дъги, където крайният върха на всяка дъга, различна от последния, е основният връх следващата.

Например, на фиг. 2.1.2 пътеки са дъги последователност:

A6, A5, A9, A8 и А4. (1)

A1, A6, A5, A9, A10, A6 и A4. (3)

Ориентирано верига (ortsepyu) е път, в който всеки дъга не се използва повече от веднъж.

Обикновено ortsepyu нарече път, в който всеки връх не се използва повече от веднъж. Например, пътя (2).

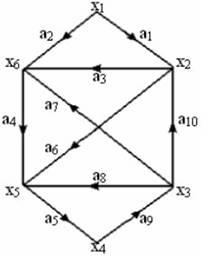
Маршрутът е ненасочена "двоен" Между другото, и това понятие се има предвид в случаите, където можем да пренебрегнем ориентирани дъги в графиката. По този начин, по маршрута е последователност от ръбове ä1 ä2. äQ, в която всеки ръб AI, с изключение на първите и последните ребра, свързани с ребра Ай-1, AI + 1 и неговите крайни върхове. Последователност на дъги:

ä2 ä4 ä8 ä10 (4)

ä2 ä7 ä8 ä4 ä3 (5)

ä10. ä7. ä4. ä8. ä7. ä2. (6)

в графиката, показана на фиг. 2.1.2 са маршрути; две точки от символа на дъга показва, че неговата ориентация е пренебрегвано, т.е. дъгата се разглежда като не-ориентирани ръб. Също така, по пътя или маршрута може да бъде представена от последователност от върха. Например, пътя (1) е както следва: x2, х5, Х4, X3, Х5, Х6. Понякога дъгите на графа са възложени на номера, наречена тегло, разходите или дължината на дъгата. В този случай, графиката се нарича графика с претеглени краища. И ако теглото дължи на върховете на графиката, а след това ние получаваме графика с претеглените върхове. Ако теглото възлага на колоната и дъги и върховете, а след това се нарича просто разумно. При разглеждане начини ц представени чрез последователност от дъги (ä1 ä2. äр), теглото му е взето номер L (μ), равен на сумата от теглата на всички дъги в М, т.е.

2.2 Алгоритъм на Дейкстра

алгоритъм на Dijkstra се изгражда най-краткия път, водещ от източник върха на други върховете на графиката (ако има такива).

По време на работа последователно алгоритъм маркирани обмислен връх. Върхът маркирани последният (засега) се намира по-близо до горната част на оригинала от всичко сам, но повече от всичко маркирани.

Първо маркирани първоначална връх; следващият вероятно ще бъде белязана от върха най-близо до източника, и в непосредствена близост до него.

Да предположим, че на даден етап е отбелязал няколко върхове. Известен най-краткия път, водещ от източника до върха с етикет. За всеки един от немаркираните върхове, направете следното:

1. Помислете за всички дъги, водещи от маркираните върховете в една немаркирана. Всяка дъга е последната дъга на пътя от първоначалното връх до немаркирана.

2. От тези кратки пътеки. И след това изберете най-краткия сред тях всички немаркираните върхове и етикет на върха, към която тя води.

Алгоритъмът ще спре, когато са отбелязани всички достижими върхове.

В резултат на Алгоритъм на Дейкстра изгражда дърво на най-късите пътища.

3 функции работят MEDIUM

Когато пишете програма да се използва Microsoft Visual C ++ среда 6.0. Тази среда позволява да пишете приложения в ++ езика C.

В хода на написването на програмата, всички оператори и от официалните езици на C ++, подчертани в различен цвят, за да ги разграничат от променливи, определени от програмист. Microsoft Visual C ++ 6.0 среда съдържа вграден компилатор.

Програмата е създадена в режим на конзола - в режима, който не разполага с графичен интерфейс.

4 софтуер ИЗПЪЛНЕНИЕ

4.1 Описание на алгоритъм и програма дизайн

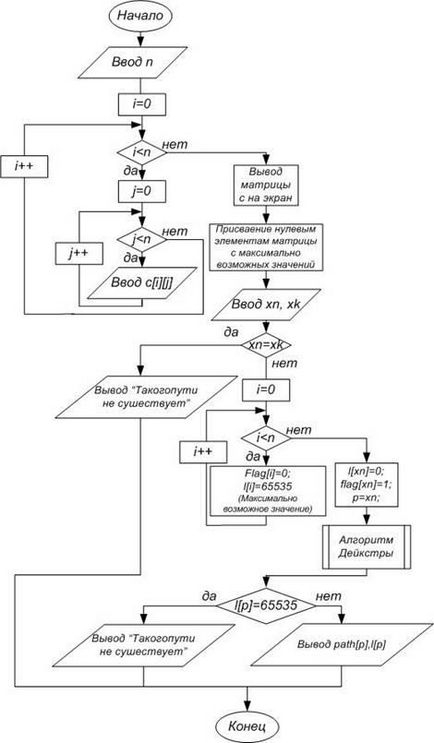
Програмата показва най-краткия път между двете върховете в графиката и неговата дължина.

Когато стартирате програмата, се показва на екрана подканени да въведете теглата на ръбовете на тест графика. Данните, въведени от потребителя, са показани под формата на матрица съседство, където краищата не съществуват са отбелязани с нули. След определен ребрата е настроен на 65 535, който се приема за безкраен.

Следващият етап на програмата е подкана да въведете номера на върха, между които е необходимо да знаете пътя. Ако началната и крайната върховете съвпадат, се показва съобщение и функционирането на програмата приключва. В противен случай, на Dijkstra алгоритъм директно, чиято схема е показан в допълнение Б.

В резултат на програмата е да се покаже върха през които минималната пътеката, както и на изхода на дължина на маршрута. Ако на пътя между дадените точки не съществуват - се появява съобщение.

4.2 Описание на използвания софтуер

Таблица 4.2.1 Определяне на променливите