Според графиката на у намерено в х, алгебра

Помислете как по графиката на у намерени в х.

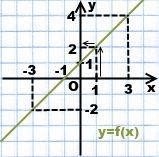
1) Използване на графиката на линейна функция. показана на Фигура 1, се намери стойността на функцията, ако той е равно на 1; 3; -3, 1; 0.

Аргументът - е х, функцията - у.

Намерете стойността на функция от стойността на аргумента - така че, за дадена стойност на х, за да намерите нещо, равно на х.

Започваме с х = 1. На абсцисата Ox намери х = 1. За да намерите съответната стойност на у, е необходимо от гледна точка на Бика да отиде нагоре или надолу, за да получите по график.

От х = 1 се покачват. От получената точка от графиката е необходимо да се движи вляво или вдясно, за да стигнем до оста Oy. В този случай, ние се връщаме в ляво и да получите ордината у = 2 (виж стрелките подпомагат посоката на движение).

Следователно, за х = 1, у = 2.

По същия начин, ако х = 3, отидете до кръстовището с графика, и се оставя да пресечната точка с ординатата ос Oy.

Ние считаме, че когато х = 3, у = 4.

Ако х = -3, да се кача на графиката на функцията, трябва да сляза, а след това - в дясно, до пресичането с оста Oy.

Когато х = -1 нагоре или надолу ход не е необходимо - тази точка е вече в графиката на функцията. Следователно, у = 0.

Добави: когато х = -1 у = 0.

Когато х = 0 отидете на График и да влезе в точка с ордината у = 2.

2) графиката на функция у = F (х) е изобразена на фигура 2.

Използване на графиката, намиране на стойността на функцията, ако той е равно на 1; 3; 5; 7; 1; -5.

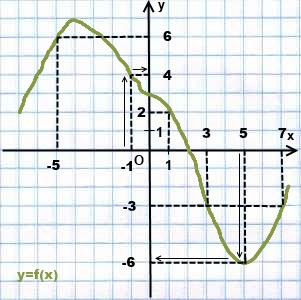
За да намерите графика функция у от х, първо е необходимо от гледна точка с абсцисата на графиката, за да се кача на движи нагоре или надолу, а след това от гледна точка на графиката, за да отидете на Oy ос, преместване наляво или надясно.

Когато х = 1 да отиде на функция графиката, след това се оставя - от Oy ос. Качваме се в точка с ордината у = 2.

Писане: когато х = 1, у = 2.

В х равно на -1 и -5 излезе пръв, а след това - в дясно.

Когато iksah равен до 3; 5 и 7 слез и си тръгна.

Имайте предвид, че различни стойности на Х може да се сравнява една стойност у:

(С х = 3 и х = 7, у = -3).