система Тегло
движение на системата, в допълнение към оперативните сили, също зависи от общото му тегло и разпределението на масата. маса на системата е равен на средната аритметична сумата от масите на всички точки или институции, съставляващи системата
В единна гравитационно поле, за това. телесно тегло всяка частица ще бъде пропорционално на теглото му. Поради това, на разпределението на масата в организма може да се съди от позицията на центъра на тежестта. Transform формули, определящи център на тежестта координати:
Получените уравнения са само масата на материала точки (частици) оформяне на тялото, и координатите на тези точки. Следователно, позицията на точка С (Хс. YC. ZC) наистина характеризиращ рана-масово разпределение в тялото или в механична B-TEM ако под. разбира съответно масата и координатите на точки на системата.
С геометрична точка, чиито координати са определени от споменатата формула, наречена центъра на маса или център на масата на системата.
Център на тежестта се определя от радиус вектор
където - векторите позиция на точки, образуващи система.
Въпреки че положението на центъра на тежестта съвпада с центъра на тежестта намира в единна гравитационно поле, тези понятия не са идентични. Концепцията на центъра на тежестта, като точка, през която линията на действие на получените силите на гравитацията, по същество има смисъл само за солидна, намирането-schegosya по еднакъв гравитационно поле. Концепцията е около центъра на масата като масови характеристики разпространение на системата, има смисъл за всяка система от материални точки, или органите, които тази концепция запазва своя смисъл, независимо от това дали тази B стволови под влияние на това, което някои сили или не.
Инерционният момент спрямо оста. Радиус на инерция-ТА.
Център на тежестта характеризира разпределението на масата на системата не е пълна. Например (Fig.32), ако разстоянието з от ос Оз всяка от идентични области А и увеличение Б със същия размер, позицията на центъра на система на масата не се променя, и разпределението на масата става различни, и това ще се отрази движение система (въртене около оста Oz при равни други условия ще бъде по-бавно).
Следователно механика въведени друга характеристика на разпределението на делене маса - инерционният момент. Inertsiitela въртящ момент (система) спрямо тази ос Оз (или аксиално инерционен момент) е скаларна равна на сумата на продукти от масите на всички точки на тялото (система) в квадратите на разстоянията от тази ос
От определението следва, че от момента на инерция (или системи) по отношение на всяка ос е положителна стойност не е равно на нула.
Имайте предвид също така, че от момента на инерция - това е геометричните характеристики на тялото, което е независимо от неговото движение.
Аксиалното инерционен момент играе подобна роля по време на въртеливото движение на тялото, което масата в транслация, т.е. че е аксиален инерционен момент IU рояк инерцията на тялото, когато Вера-внимателно движение.
Според формула инерционен момент, равен на сумата на инерционни моменти-ING всички негови части, в сравнение с една и съща ос. За ML-солна материал точка тучни-dyascheysya на разстояние часа от оста.
Често по време на изчисленията се използва концепцията за радиус на въртене. Body радиус от инерцията около оста Oz е линейна стойност. определен от уравнението
където М - маса на тялото. От определението следва, че радиус на въртене е разстоянието от геометричния оста Oz точката, в която е необходимо да се концентрира цялата телесното тегло на инерционен момент на тази една точка е равна на инерционния момент на тялото.
В случай на твърдите тези, ла, това бяха разделили на елементарни части, откриваме, че в границата на сумата на равенството, на свой ред неразделна. В резултат на това като се има предвид какво. където - плътност и обем V- ние получаваме
Интегралът е през целия обем V на тялото, и плътността и разстояние з са зависими от координатите на точки на тялото.
В моменти на инерция на някои хомогенни тела:
1.Tonky хомогенна прът с дължина L и масата М. изчисли своя инерционен момент по отношение на Az-telno ос, перпендикулярна на пръта и proho-dyaschey чрез своя край А (фиг. 33).
Режисьор заедно AB координатна ос брадва. След това за всеки елементарен сегмент на DX стойност дължина от Н = х, и масата, където - дължината на единица маса на пръта. В резултат на това
Подмяна стойността си, ние най-накрая получи:
2. тънък еднакъв радиус кръгъл пръстен R и масата М. Ние намери инерционен момент около оста Cz, перпендикулярна на равнината на пръстена и минаваща през центъра (Fig.34 а). Тъй като всички точки на пръстените са в региона Cz ос HK = R, тогава
Следователно, за пръстена
Очевидно е, че същият резултат се получава по време на масово тънък цилиндричен корпус М и инерционен радиус R, но по отношение на неговата ос.
3. Кръгла хомогенна плоча или цилиндър радиус RA-R и изчисляване на маса инерционен момент М. кръгъл PLA-Щина относително Cz ос, перпендикулярна на плочата и proho-dyaschey през неговия център (вж. Fig.34, а). За да се различава този елементарен пръстен с радиус R и ширина р (fig.34, б).
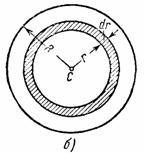
Размерът на този пръстен е и масата, където - теглото на единица площ на плочата. След това, в продължение на избраните елементарни пръстени ще
докато за цялата плоча. Подмяна стойността си, ние най-накрая
Същата формула ще очевидно за момента на инерция на кръгов цилиндър с еднаква маса М и радиус R около оста си Оз (ric.34, в).
4. правоъгълна плоча, конус, топка. Пропускането на изчисленията, ние представяме формули, определящи инерционни моменти следните органи:
. А) непрекъснато правоъгълна плоча на масата М със страни а и AB = BD = В (х-ос по протежение на страничната AB Y ос - заедно BD):
б) непрекъснато прав кръгов конус на маса М с база радиус R (Z ос е насочена по оста на конуса)
г) твърда маса М и радиус R на топка (Z ос е насочена по диаметър)