Преходът към друга координатна система - studopediya
Ние прегледахме трансформацията на геометрични обекти, определени в конкретна Декартова координатна система. Но в много случаи е удобно да се помисли за едни и същи обекти в различни координатни системи, като тяхното описание може да бъде по-прост. Най-простият пример - задача да координира кутията: най-лесният начин да направите това в координатна система, в комбинация с един от върховете му с оси, насочени по ръбовете. В тази връзка, ние обсъждаме въпроса, как да промените координатите на точката, в прехода от една декартова координатна система в друга.
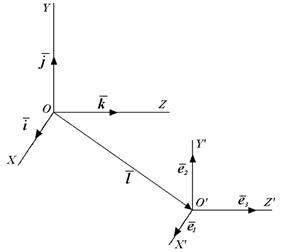
Фиг. 3.9. Две координатна система в пространството
Нека единични вектори на първата координатна система са посочени и координатните оси -. Ние също въведе координатна система, които означават векторите на устройството и оси -. Тази система има своя произход и неговите ос посоки. Ние вярваме, че и в двете координатни системи единични вектори образуват лявата ръка тризнаци (фиг. 3.9).
Първо, помислете за ситуация, когато точката съвпада с точката. Вектори могат да бъдат определени в първата координатна система, разпределяйки ги векторите:
Ако първата точка има координати система, а втората система - тогава, очевидно,
Като вътрешен продукт, съотношението на вектори, ние получаваме връзката между стойностите координатните в различни системи:
Тези отношения могат да бъдат написани в матрична форма
или вектор нотация
Да приемем, че вторият координатна система се получава от първия с ъгъл на въртене около оста. след това
По този начин, при завиване нова координатна система на координатите на точките, получени чрез умножаване на матрицата на въртене към противоположния ъгъл на първоначалните векторни координати.
Ако новата координатна система се получава чрез прехвърляне от старата към вектора, очевидно е, че новите координати на точки, дадени от формулите
Сега може да се помисли за състава на две координатна система трансформации - превод и въртене. След това точките координатите трансформирани с формула