Предикати и quantifiers
Пропозиционални логика се прилага прост декларативни изявления, в които основните отчети - било истина или лъжа. Отчети, съдържащи един или повече променливи, може да е вярно за някои стойности на променливите и неверни към другите.
По сказуемото е изявление, съдържащо променливи, които оценява вярно или невярно, в зависимост от променливите.
Например, изразът "х число, отговарящо на връзката х = х 2" е предикат, както е вярно за х = 0 или х = 1 и фалшиво във всички останали случаи.
Предикати се прехвърлят всички операции (логично сухожилие), които правим с твърденията. Истината на съединение сказуемото зависи от стойностите на променливите, включени в него.
- декларация, съдържаща променлива.
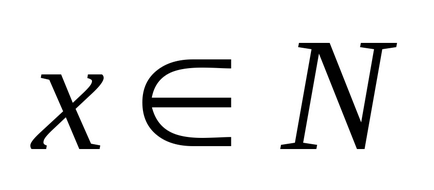
Концепцията за квантор
Има логически оператори quantifiers. чието използване за предикат ги превръща в неверни или верни твърдения.
Твърденията, че някои имот притежава "всички" на обектите, наречена квантор "общност" и посочва .
Се твърди, че "има (там)," най-малко един обект, който има този имот се нарича квантор "съществуване" и посочва .
Включително quantifiers в предикат, ние го превърне в свое изявление. Затова предикат количествено може да е вярно или невярно.
Казаха x Р (х) означава, че областта на истина предикат Р (х) съвпада с обхвата от стойности на променливата х. ( "За всички стойности на (х) е вярно").
Казвайки x P (х) означава, че в областта на истината предикат P (х) не е празна ( "Има (х), за които твърдението е вярно").
1)
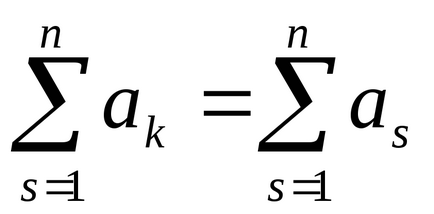
2)
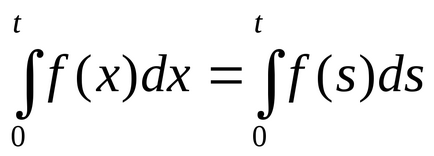
3)
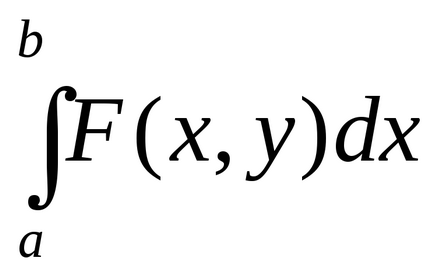
методически указания
Обучението на компютърно-базирани е логично грамотност. Логически основи грамотност е възможността за производство на трансформацията формули са еквивалентни, а това изисква задълбочено разбиране на Пропозиционални език логика.
Всеки език за програмиране трябва да съдържа логически connectives оператори, т.е. Той съдържа Пропозиционални логика. Компютри за всякакви цели и сложността на логически блокове съдържат :. дизюнктивен, конюнктива и друг проект, синтез, работа на която се основава на законите на Пропозиционални логика.
Пример 1: Виж изложението, състояща се от три атома, таблица истина е:
Решение. За да намерите изявление с предварително определена маса истина, то е необходимо да се вземат основната дизюнкцията на съюзите на тези линии, които в дадената таблица истина отговаря на стойността 1. В този пример, се изисква декларация ще бъде:
Този метод на решение може да бъде отложено в случай на наш променливи.
Пример 2: Нека P (х) - предикат "х - реално число, и
х 2 + 1 = 0. " Казано с думи казваха: х. F (х), и се определя истина стойност.
Решение. Това твърдение може да се чете, както следва: има
реално число х удовлетворява уравнението х 2 + 1 = 0. От площада на всяко реално число не е отрицателен, т.е.. Д. X 2 0, получаваме, че х 2 + 1 1. Поради това, изявлението х. F (х) е погрешно.
Отрицанието на изявлението на този пример, може да се запише като:
не х. F (х). Това е естествено вярно твърдение, което означава, че не е реално число х задоволяване х 2 + 1 = 0. С други думи, за всяко реално х,
х 2 + 1 0. В символна форма, това може да се запише като h не P (х).
За обща предикат Р (х) е следната логическа еквивалентността:
не h. F (х) х не е Р (х);
не х F (х) х. F (х).
Някои трудности възникват, когато изказването участва повече от един квантор.
Пример 3: Да предположим, че х и у - са реални числа, и Р (х, у) представлява предиката х + у = 0. Express всеки от думи и изказвания определяне на тяхната валидност.
1) xy твърдението: Р (х, у) се казва, че за всяко реално число X, съществува реално число Y така, че х + у = 0. Очевидно е вярно, тъй като независимо от броя вземем х броя на у = h плати равенство х + у = 0 в правилната идентичност.
2) u изказване. h P (X, Y) се чете, както следва: налице е реално число от че за всяко реално число х, равенството х + у = 0. Това със сигурност не е такъв не съществува реално число у които да притежават. Следователно, твърдението е погрешно.