Правила за изграждане на магически квадрати компилация от магически квадрати

След няколко години с родителите ми, аз отидох до морето срещнал момичето, което е обичал судоку. Аз също исках да се учи, а тя обясни как да го направя. Този урок аз наистина го харесва, и тя се превърна в мой т.нар хоби.

След като ми предложиха да участват в научно-практическа конференция, аз веднага избра темата на "магически квадрати". В тази работа съм включил исторически материали, сортове, правила за създаване на игра-пъзел.
Магията квадрат.

Магически или магически квадрат е квадратна матрица попълнено числа п, така че сумата от числата във всеки ред, всяка колона и от двете диагонали е същото. Нормално се нарича магически квадрат, изпълнена с числа от 1 до п.

съществуват магически квадрати за всички поръчки, с изключение на п = 2, въпреки че при п = 1 е тривиална - квадрат се състои от един номер.

Сборът от числата във всеки ред, колона и диагонал. Той призова магически числа. М. магически постоянен нормален магически квадрат зависи само от п и даден от уравнение.

Тази таблица има забележителен имот. Добавянето на броя на първата колона: 4 + 3 + 8 = 15.tot същия резултат се получава чрез добавяне на броя на втората и третата колони, както и. Той се получава чрез добавяне на номерата на някой от трите реда. Не само това, се получава същия отговор 15, ако броят на сгънати всяка от двете диагоналите: 4 + 5 + 6 = 8 + 5 + 2 = 15.

Може би тази легенда китайците измислиха, когато ние открихме, на мястото на цифрите от 1 до 9 с такъв забележителен имот. Фигура те нарича "ло-шу" и се възприема като символ на неговата магия и заклинания за използване при. Така че сега всеки квадратен маса, съставена от числа и има свойството да се нарича магически квадрат.

SQUARE намерени в Khajuraho (Индия).

Най-ранното уникална магия площада се намира в надписа на единадесети век в индийския град Каджурахо.

Това е първата магия площада, позовавайки се на разнообразието от така наречените "дяволски" квадрати.

Магически квадрант Ян Hueya (Китай)

В математик на XIII век Ян Хюи заема проблемът за методите на конструиране на магически квадрати. тогава Неговите изследвания са продължени от други китайски математици. Ян Хюи счита магически квадрати са не само третата, но големи поръчки.

Някои от неговите площади са доста сложни, но той винаги е дал правилата за тяхното изграждане. Той е в състояние да изгради магически квадрат на шестия ред.

Площадът на Albrehta Dyurera

4х4 магически квадрат, показан на А. Дюрер гравиране "Меланхолия I», се счита за най-ранните в европейското изкуство. Две средни числа в най-долния ред посочват датата на създаване на картината (1514)

Сума от числата във всяка хоризонтална, вертикална и диагонална равен на 34. Тази сума също се намира във всички краища на квадрата на 2x2, в централен квадратен (10 + 11 + 6 + 7), на квадрата на клетките ъгъл (16 + 13 + 4 + 1), в квадрати конструирани "люлка кон" (2 + 8 + 9 + 15 и 3 + 5 + 12 + 14), правоъгълници, образувани от двойки вторични клетки върху противоположните страни на (3 + 2 + 15 + 14 и 5 + 8 + 9 + 12) .Most допълнителни симетрии, свързани с факта, че сумата на две централно симетрично разположени брой се равнява на 17.
Площади Хенри Е. Dudeney и Allan W. Johnson мл.

Ако квадратна матрица на N х N се съхраняват свободно естествени числа, тогава магически квадрат - неконвенционални. По-долу са две такива магически квадрати, пълни с най-вече прости числа. Първият (Фигура 3) има реда п = 3 (квадрат Dudeney); втори (фиг.4) (4x4) - площад Джонсън. И двете са разработени в началото на ХХ век.

магически квадрат Дяволското

Devil магически квадрат - магически квадрат, което съвпада с магически постоянна сумата от броя на разбито диагонал (диагонал, които са образувани чрез прегъване на квадратен в тора) в двете посоки.

Тези квадрати се наричат ​​също pandiagonalnymi.

Има 48 диаболични магически квадрати 4x4 до ротации и разсъждения. Ако вземем под внимание все повече и повече симетрия - торични паралелни преводи, а след това ще има само 3 различава значително квадрат:

Въпреки това, е доказано, че (Фигура 7) прост прегрупиране на номера получава първите две квадратчета (Фигура 5, 6). Това е трети вариант е базовата диаболичен квадрат, от който различните трансформации могат да изградят всички останали.

Pandiagonalnye квадрати са за нечетен ред п> 3, в произволен ред двойно паритет п = 4k (к = 1,2,3, ...) и не съществуват за един четност за п = 4к + 2 (к = 1,2,3, ...) ,

Pandiagonalnye квадратите на четвъртия ред са редица допълнителни свойства, за които те се наричат ​​перфектно. Pandiagonalnyh добра площади на нечетен ред не съществува. Сред pandiagonalnyh площади паритет над 4 са перфектни.

Pandiagonalnyh петия ред квадрати 3600. С оглед на торични паралелни преводи има 144 различни pandiagonalnyh квадрати. Един от тях е показано по-долу.

Правила за изграждане на магически квадрати

Намери всички магически квадрати на наш ред е възможно само, п = следователно 3,4 са от голям интерес и по-специално процедурата за изграждане на магически квадрати за п> цялата 4.Prosche дизайн за вълшебната площад на нечетен ред. Тя трябва да бъде в клетка с координатите (х, у), поставени номера.

Даже по-лесно да се извърши строителството следва, считано матрица н х n.Vnutri вградената етап диамант. Той напусна килията нагоре диагонално попълнено последователно поредица от числа. Определена стойност на централната клетка В.

След това, в магически ъглите на квадратните стойности са както следва: горния десен клетката С-1; долния ляв клетка C + 1; С долния десен клетъчно-N; горния ляв клетка C + п.

СЪСТАВЯНЕ магически квадрати.

Как тогава да направи магически квадрати?

Създаване на магически квадрат "Ло Шу".

Задача. 3x3 квадрат, образувана от цифрите от 1 до 9, така че сумата от числата във всеки ред, колона и диагоналите са равни.

Решение: Ние реши проблема без да се прибягва до сортиране един по един всички пермутации на 9 цифри 9 клетки (броят на такива договорености от един и същи 362880). Ние твърдим. Сумата на всички номера от 1 до 9: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Това означава, че на всеки ред и всяка колона трябва да е равна на сумата от номера: 45: 3 = 15. Но ако обобщим всички числа във втория ред и колона и двата диагонала, всеки номер ще остане един път, с изключение на центъра, който ще влезе четири пъти. Следователно, ако ние означаваме с х централната номер, след това равенство 4 * 15 = 3 * 15 + 3. Следователно х = 5, която е в центъра на масата трябва да бъде номер 5.

Сега, имайте предвид, че броят 9 не може да стои в ъгъла на масата, например в горния ляв ъгъл. В края на краищата, а в противоположния ъгъл стоеше числото 1, и на първия ред и колона остава една комбинация - номера 4 и 2. Това означава, че 9 се намира в средата на някои крайни редове или колони (тук в средата на първия ред). Две други номера на реда са 4i2 и третата колона на средния брой трябва да е 1 = 9.5.15. В една и съща линия 1 трябва да бъде броят 8 и 6. По този начин, магията площада е почти пълна и лесно да се намери място за останалите цифри. Резултатът е квадрата на "Луо Шу".

Разбира се, за 9, за да изберете други три места, а след избора на място за този номер две възможности за подреждане на номера 4 и 2. получени общо 4 * 2 = 8 различни магически квадратите на три реда и три колони (или, тъй като математиката квадратите на третия ред). Всички тези квадрати може да се намери в "Ло Шу" или превръщането на площада на 180.90 или 270. Друга възможна опция отразявайки.

Създаване на магически квадрат

Цел: Създаване на 4х4 магически квадрат на номера от 1 до 16, така че сборът от числата във всеки ред, колона и диагоналите са равни.

Решение. Сумата на всички номера от 1 на 16: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136. Това означава, че на всеки ред и всяка колона трябва да е равна на сумата от номера: 136: 34 = 4. Но ако обобщим всички числа, и второ, в реда и колоната, и двата диагонала, всеки номер ще остане един път, с изключение на централната, които ще бъдат включени два пъти. Тези номера ще 10,11,6,7. След това ние доставяме оставащия брой останалите клетки в 1,2,3,4,5,8,9,12,13,14,15,16

Площадът на Albrehta Dyurera
Судоку.

Преведено от "числото" японската "СУ" означава и "акостира" - ". Застанал сам"

Няма нужда да се отгатне или капково в книгите - само логика и внимание!

Цел: Да се ​​запълнят празните клетки с номера от 1 до 9, така че всеки ред и всяка колона във всяка от 9 блокове 3x3 фигура не се повтаря.

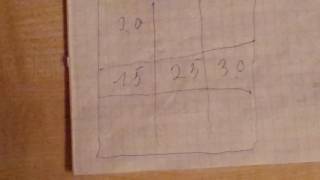
Нека да погледнем на специален номер. Липсва само две цифри: 1 и 2.Vzglyanem първата празна клетка надясно. Можем ли да пиша там един? Не. Поради тази колона 1 е вече там, и повтори тези числа в колона не могат. Така че, в тази клетка, ние може да влезе само 2 да го направи. Сега ние просто трябва да въведете номера 1 в празно, последната клетка на реда, както и броя на запълнени.

За да стане още по-интересно, можете да създадете судоку на различни нива на трудност:

-Лесно *, ** - средна, *** - трудно, **** - много трудно, **** - superslozhnyh.

Разликата в нивата е, че броят на цифрите в блока се увеличава.

Първо - не разполагат с достатъчно на брой 2.3.

II - 4, третият - 5,4, четвъртата - 6, петият - 6.7.

Черните клетки се наричат ​​Kakuro легенда. Те са разделени с наклонена черта и съдържа един или два номера. Числото в горния десен ъгъл принадлежи към съседния хоризонтален единица клетка (А) и в долния ляв - за вертикално (B).

Цел: Да се ​​влиза в празните клетки с номера от 1 до 9tak че тяхната сума съответства на размера на блока в легендата. Устройството не може да бъде два еднакви цифри! Така броят 4 в легендата може да устои само на 1 март, вместо цифри 2 и 2.

Първо проверете дали малка сума - това е лесно да се разлага на телефонните номера. Като начало 3. В този случай, комбинациите могат да бъдат или "1 + 2" или "2 + 1". На трето място, разбира се, не се дава.

4 може да съответства на броя на комбинациите от "1 + 3" или "3 + 1" (но не 2 + 2). Така че, в първото поле може да бъде само броят 1. Сега можем да попълните правилно двата блока: "1 + 2" и "1 + 3".

Нека да разгледаме 4 в последния легендата. Изпълнения тук са същите: "3 + 1" и "1 + 3". Номер 3 в хоризонтален блок е вече там, и единственото възможно решение - номер 1.

И сега можем да се запълнят всички други клетки. Съвет: вписва в ъглите на възможните комбинации на броя на клетките, и като пълнеж премине от числа, които не са включени.

(Регионален център за деца с изявени дарби и младежта.

Вътрешен кръг на конкурса "Млад експерт по математика"

В квадрата, съставен от 9 клетки, да се постави номер от 1 до 9, така че сумата от числата на всеки вертикален ред във всеки хоризонтален ред и всеки диагонален са равни.

Създаване на моята работа, аз разшири познанията ми за концепцията на магически квадрати, за правилата на сътворението си, да научи историята на това как те са създадени, научих много нови думи научих да работя с литературата, реши и да се създаде магически квадрати.

IY Depman; N.Ya.Vilenkin "За математика учебник страници"

София "Просвещение", 1989.

VP Trutnev "Мисли, реши, предполагам!" София "Просвещение", 1970.

"Lisa" (на кръстословици, судоку, Kakuro)

предишните статии

следваща статия

Всички материали в секцията "Други есета"

Благодаря Ви много. Много интересна информация за магически квадрати.