Определяне на чин матрица

За да работите с концепцията за ранг на матрица, ние се нуждаем от информация по темата "алгебрични допълнения и непълнолетните. Видове непълнолетните и кофактори." По-специално това се отнася за термина "малка от матрицата." като ранга на матрицата стане откриване е през непълнолетните.

Рангът на матрица се нарича максимална реда на своите непълнолетни лица, сред които има най-малко една нула.

Еквивалентно матрица - матрица, чиито редици са равни.

Нека обясним по-подробно. Да предположим, че сред малолетни и непълнолетни лица от втори ред да има поне една различна от нула. И всички малолетни и непълнолетни лица, чиито ред е по-голяма от два, са равни на нула. Заключение: ранг е 2. Или, например, сред непълнолетните на заповед десет да има поне една нула. И всички малолетни и непълнолетни лица, чиито ред е по-висока от 10, са равни на нула. Заключение: ранг е 10.

Определени ранга на матрицата $ A $ като: $ \ звънна A $ и $ R (A) $. Място нула матрица $ O $ приема да бъде нула, $ \ позвъни О = 0 $. Спомнете си, че за формиране на матрицата изисква минимални заличени редове и колони - но да изтриете редове и колони над матрицата се състои невъзможно. Например, ако $ F $ матрица е с големина от 5 $ \ пъти $ 4 (т.е., съдържа 5 редове и колони 4), максималната реда на своите непълнолетни равна на четири. Непълнолетните форма пети ред няма да успее, защото 5-те колони се изисква за тях (и ние имаме общо 4). Това означава, че ранга на матрицата $ F $ не може да бъде повече от четири, т.е. $ \ Rang F≤4 $.

В по-общ вид на по-горе означава, че ако матрицата съдържа редове $ m $ и $ п $ колони, след това си ранг да не надвишават ниските на номера $ m $ и $ п $, т.е. $ \ Rang A≤ \ минути (m, п) $.

По принцип самото определение за ранг трябва да бъде методът на местоположението му. Процесът на намиране на матрицата да се определи в ранг може да бъде схематично представена, както следва:

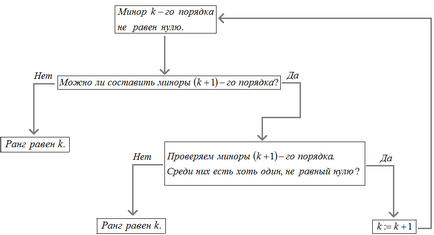
Ще обясня тази схема в по-големи подробности. Ние започваме да говорим от началото, т.е. малолетни и непълнолетни с матрица от първи ред $ A $.

1. Ако всички непълнолетни първи ред (т.е., елементите на матрицата $ A $) са равни на нула, тогава $ \ позвъни А = 0 $. Ако има поне един, различен от нула сред малолетни и непълнолетни лица от първи ред, а след това $ \ звънна A≥ $ 1. Ние се пристъпи към проверка на непълнолетните от втори ред.
2. Ако всички вторите непълнолетни лица ред са равни на нула, а след това $ \ звънна A = 1 $. Ако има поне един, различен от нула сред малолетни и непълнолетни лица от втори ред, тогава $ \ звънна A≥ $ 2. Ние се пристъпи към проверка на третия ред на непълнолетните.
3. Ако всички малолетни и непълнолетни лица от трети ред са равни на нула, а след това $ \ звънна А = 2 $. Ако има поне един, различен от нула сред малолетни и непълнолетни лица от трети ред, тогава $ \ звънна A≥ $ 3. Ние се пристъпи към проверка на малолетни и непълнолетни лица четвъртия ред.
4. Ако всички непълнолетни лица на четвъртия ред са равни на нула, а след това $ \ звънна А = 3 $. Ако сред малолетни и непълнолетни четвъртия ред има най-малко една различна от нула, а след това $ \ звънна A≥ $ 4. Ние се пристъпи към проверка на малолетни и непълнолетни лица пети ред, и така нататък.

Какво ни очаква в края на тази процедура? Възможно е, че сред непълнолетни от порядъка к-то има най-малко един не-нула, и всички непълнолетни (к + 1) та цел ще бъде нула. Това означава, че K - максималната реда на непълнолетните, сред които има най-малко една различна от нула, т.е. Ранг е равен на к. Може ситуацията е различна: сред непълнолетни на к-тия ред ще има най-малко една ненулева и непълнолетни (к + 1) няма да може да се образува на ред. В този случай също равен на ранга к. С една дума, по реда на последната не е нула непълнолетния компилиран и ще бъде равен на ранга на матрицата.

Ние се обръщаме към примерите, в които процесът на намиране на матрицата да се определи в ранг ще бъдат илюстрирани графично. Още веднъж искам да подчертая, че в примерите на тази тема, ние ще намерим ранга на матрицата, с помощта на определяне на ранг. Други методи за изчисление (ранг матрица метод ресни непълнолетни. Изчислителен метод ранг матрица елементарни преобразувания) се разглеждат в следните теми.

Между другото, не е необходимо да се започне процедурата за намиране на ранг непълнолетни, най-малкият ред, както в примерите №1 и №2. Можете да отидете директно на непълнолетните от по-висок ред (вж. Пример №3).

Намери ранг на матрица $ A = \ ляв (\ започне 5 0 -3 0 2 \\ 7 0 -4 0 3 \\ 2 0 -1 0 1 \ край \ вдясно) $.

Тази матрица е с размер на 3 $ \ пъти $ 5, т.е. Той включва три реда и пет колони. От цифрите 3 и 5, минималното е 3, следователно, с ранг на $ A $ е не по-голяма от 3, т.е. $ \ Rang A≤ $ 3. И това неравенство е очевидно, тъй като непълнолетни, четвърти формата за поръчка вече не можем да, - за тях ще трябва 4 реда, а ние имаме само 3. Ние се обръщаме директно към процеса на намиране на даден ранг на матрица.

Сред непълнолетни първи ред (т.е. между елементите на матрицата $ A $) е нула. Например, 5, -3, 2, 7. Като цяло, ние не се интересуват от общия брой на ненулеви елементи. Има поне един ненулев елемент - и това е достатъчно. Тъй като сред непълнолетните от първи ред да има поне една различна от нула, а след това ние се заключи, че $ \ звънна A≥ $ 1 и отиде да провери непълнолетните от втори ред.

За да започнете да разследва втория непълнолетните ред. Така например, в пресечната точка на линиите №1, №2 и колони №1, №4 са елементи като непълнолетен: $ \ лява | \ започне 5 0 \\ 7 0 \ край \ дясна | $. Това определящ всички елементи на втората колона на нула, и следователно се детерминанта е равно на нула, т.е. $ \ Left | \ започне 5 0 \\ 7 0 \ край \ дясна | = 0 $ (виж имот №3 в имотите предмет на детерминанти.). Друга възможност е да се изчисли банално този фактор, като се използва формулата №1 на раздела за изчисляване на детерминантите на втория и третия поръчките.

$$ \ лява | \ започне 5 0 \\ 7 0 \ край \ дясна | = 5 \ cdot 0-0 \ cdot 7 = 0. $$

Първо ние тествахме Мала втори ред е равна на нула. Какво означава това? Фактът, че необходимостта от по-нататъшно провери непълнолетните от втори ред. Или всички те са нула (и след това в ранг е равен на 1), всеки един от тях има най-малко един непълнолетен, различна от нула. Нека се опитаме да приложат по-добър избор от написването Мала на втория ред, елементите на които са разположени в пресечната точка на линиите №1, №2 и колони №1 и №5: $ \ лява | \ започне 5 2 \\ 7 3 \ край \ дясна | $. Ние откриваме значението на този незначителен втори ред:

$$ \ лява | \ започне 5 2 \\ 7 3 \ край \ дясна | = 5 \ cdot 3-2 \ cdot 7 = 1. $$

Това непълнолетен не нула. Заключение: сред малолетни и непълнолетни лица от втори ред да има поне една различна от нула. Затова $ \ звънна A≥ $ 2. Необходимо е да се пристъпи към разследването на малолетни и непълнолетни лица от трети ред.

Ако непълнолетните лица да формират третия ред ще изберем колоната или колона №2 №4, че такива непълнолетни лица ще бъде нула (защото те ще съдържа нула колона). Остава да се провери само един непълнолетен третия ред, елементите на които са разположени в пресечната точка на колона №1, №3, №5 и линии №1, №2, №3. Пишем тази незначителна и намери своето значение:

$$ \ лява | \ започне 5 -3 2 \\ 7 -4 3 \\ 2 -1 1 \ край \ дясна | = -20-18-14 + 16 + 21 + 15 = 0. $$

Така че, всички непълнолетни от третия ред са равни на нула. Последно съставен от нас не е нула непълнолетен е вторият ред. Заключение: максималната реда на непълнолетните, сред които има най-малко една различна от нула, е равно на 2. Ето защо, $ \ звънна А = 2 $.

Намери ранг на матрица $ A = \ ляв (\ започне -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ край \ вдясно) $.

Имаме квадратна матрица на четвъртия ред. Сега, ние се отбележи, че в ранг на тази матрица е не повече от 4, т.е. $ \ Rang A≤ $ 4. Качваме се свежда до намиране на ранг на матрица.

Сред непълнолетни от първи ред (т.е. между елементите на матрицата $ A $) има поне един ненулев, така $ \ позвъни A≥ 1 $. Ние се пристъпи към проверка на непълнолетните от втори ред. Така например, в пресечната точка на линиите №2, №3 и колони №1 и №2 се получи малка от втори ред: $ \ напусна | \ Започнете 4 \\ -2 -5 0 \ край \ дясна | $. Нека да го изчисли:

Сред непълнолетните от втори ред да има поне една различна от нула, така че $ \ звънна A≥ $ 2.

Нека да преминем към непълнолетни от трети ред. Ние откриваме, например, малки елементи, които се намират в пресечната точка на редове №1, №3, №4 и колони №1, №2, №4:

$$ \ напусна | \ Започнете -1 3 \\ -3 -5 0 0 \\ 9 7 -7 \ край \ дясна | = 105-105 = 0. $$

Тъй като непълнолетен трети ред е равна на нула, тогава ще трябва да разследва непълнолетен третия ред. Или те са равни на нула (тогава ранг е равен на 2), всеки един от тях има най-малко една различна от нула (тогава те ни разкриват непълнолетните от четвърти ред). Помислете за реда на второстепенен трета, елементите на които са разположени в пресечната точка на реда №2, №3, №4 и колони №2, №3, №4:

$$ \ напусна | \ Започнете -2 5 1 \\ 0 -4 0 \\ 7 8 -7 \ край \ дясна | = -28. $$

Сред непълнолетните от трети ред да има поне една различна от нула, така че $ \ звънна A≥ $ 3. Ние се пристъпи към проверка на малолетни и непълнолетни лица четвъртия ред.

Всяка малка четвърти ред се намира в пресечната точка на четири линии и четири колони от $ A $. С други думи, непълнолетен четвърти ред - това е най-определящ фактор на матрицата $ A $, тъй като това е само една матрица, съдържаща 4 реда и 4 колони. В детерминанта на тази матрица се изчислява в Пример №2 тема "Намаляване детерминанта на ред. Разширяването на детерминанта по ред (колона)". така просто да вземем крайния резултат:

$$ \ напусна | \ Започнете -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ край \ дясна | = 86. $$

Така Мала четвърти, за да не е нула. Непълнолетните пети формуляр за поръчка ние не можем. Заключение: най-висока степен на малолетни и непълнолетни лица, сред които има най-малко една различна от нула, е равно на 4. Резултатът: $ \ звънна А = 4 $.

Намери ранг на матрица $ A = \ ляв (\ започне -1 0 2 -3 \\ 4 -2 5 1 \\ 7 -4 0 -5 \ край \ вдясно) $.

Сега ние се отбележи, че тази матрица съдържа 3 реда и 4 колони, така че $ \ звънна A≤ 3 $. В предишните примери, ние започваме процеса на намиране ранг внимание непълнолетни, най-ниската (първи) ред. Тук се опитваме да проверим веднага непълнолетните възможно най-добрия ред. За матрица $ A $ на тези непълнолетни лица са три. Помислете за дребни елементи от трети ред са разположени в пресечната точка на линиите №1, №2, №3 и №2 колони, №3, №4:

$$ \ напусна | \ Започнете 0 2 -3 -2 \\ 5 1 \\ -4 0 -5 \ край \ дясна | = -8-60-20 = -88. $$

По този начин, най-високият ред на непълнолетни, между които има най-малко един ненулев, равно на 3. Следователно, ранга на матрицата е 3, т.е. $ \ Звънна = 3 $.

Като цяло, намери ранга на матрицата да се определи - в общия случай проблемът се отнема доста време. Например, матрицата е относително малък $ 5 \ пъти 4 $ 60 има втори непълнолетни ред. И дори ако 59 от тях са равни на нула, 60-непълнолетният може да бъде различна от нула. След това трябва да проучи непълнолетните от третия ред, който в тази матрица от 40 броя. Обикновено те се опитват да използват по-малко тежки методи, като метод на ресни непълнолетни или метод еквивалентни трансформации.