Операции на вектори в координати

С вектора е определено в правоъгълна координатна система за извършване на действия още по-лесно, отколкото със своите геометрични изображения. В тази статия ще покажем как се изпълняват операциите на добавяне на вектори и умножение на вектор с число, ако знаете, техните координати и анализира в детайли решения на примера.

Нека равнината, определена правоъгълна Декартова координатна система Oxy. Помислете векторите. Тези вектори могат да бъдат разградени от координатните вектори и други подобни, които е доказано, в статията на вектора координати в декартова координатна система.

Намерете сбора на вектори, както и продукта на вектор от всяко реално число.

От свойствата на операции на вектори. ние имаме следното равенство

В дясната страна на тези уравнения представляват вектори и разширяване на координатните вектори и следователно вектори имат координати и съответно.

По същия начин, за векторите, определени в правоъгълна координатна система Oxyz в триизмерното пространство, можем да запишем

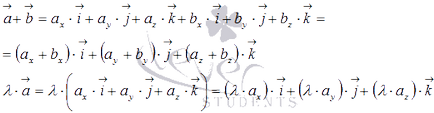
Ето защо.

По този начин, координатите и вектор сумата на равни на векторите на сумата и съответните координати,

и координатите на вектор продукта от броя равни на съответните координати на вектора умножени по брой в предварително определена координатна система.

Ако искате да намерите координатите на сума от няколко вектори, те ще бъдат равни на сумата на съответните координати на всеки от векторите.

Нека разгледаме няколко примера за решения.

Извършване на действието на допълнение вектор и както и да получите координатите на вектор произведението от броя.