Огъване Анализ на статично неопределими греди
8.10.1. единичен лъч
Има статично неопределен лъч, в който всички реакции, които не могат да се определят от уравненията на статиката сами. Така, лъчът на фиг. 8.44 и има три неизвестни реакция. , и статични и само две уравнения и. И за лъч на фиг. 8.44, б четири неизвестни реакции:. , и. Броят на уравнения на статиката, както и в предишния случай, същите две условия са равни на нула, всички моменти по отношение на свързването препратката.
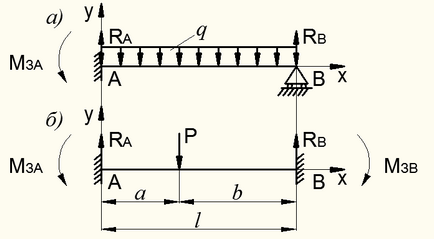
Фигура 8.44 - на статично неопределен, един период _balki
Разликата в броя на отговорите и на броя на статичните уравнения нарича степента на резервиране на гредата.
За греди ris.8.44, и степента на съкращение е. каза, че веднъж гредата да е статично несигурно. За греди ris.8.44 б. т.е. статично неопределен лъч два пъти. По този начин, статично неопределими греди са така наречените "екстра" неизвестен по отношение на броя на уравненията на статиката. За да ги определи с помощта на условието за съвместимост на деформация, изготвянето на които се разглеждат следните примери:
Пример 9.9.1. Разкриване на съкращения и изчисляване на огъване лъч (ris.8.45, както и).
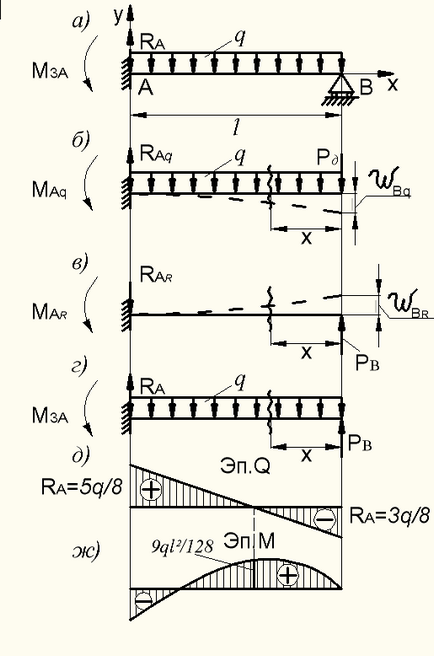
където - отклонение на лъча на р натоварване за отстраняване на психичното подкрепа В (виж фигура 8.45, б ..); - отклонение на лъча от силата (реакция) (виж Фигура 8.45 в ..).
Изчисляваме деформацията на базата на интегрална Mora.
Т mnQZnU8x9mMIP7jiCJJXAwUPAjXS4dQr2fgi / OfDsNSz9lIXQXZMqkHGjJU + 0OiZGzh0fd6Hvk2P 7cmh2CGxBoYpx61EoQbzhZIOJzyj9vOGGUGJeq2xOfPxZOJXIiiT6VmCijm15KcWpjlCZdRRMogr F9bI563hEptYysCv7 / aQySFnnNxA + 2Н / Gqc6sHrz79g + RsAAP // AwBQSwMEFAAGAAgAAAAhAIHn VGPgAAAACwEAAA8AAABkcnMvZG93bnJldi54bWxMj8FOg0AQhu8mvsNmTLzRBYKtRZbGaOzNGNFU jws7ApGdJey2xT59x5MeZ + bLP99fbGY7iANOvnekIFnEIJAaZ3pqFby / PUW3IHzQZPTgCBX8oIdN eXlR6Ny4I73ioQqt4BDyuVbQhTDmUvqmQ6v9wo1IfPtyk9WBx6mVZtJHDreDTON4Ka3uiT90esSH Dpvvam8V + CZe7l6yavdRyy2e1sY8fm6flbq + MU / vQAScwx8Mv / qsDiU71W5PxotBQZQlN + weFGTp CgQTUbLmRc3oKk5BloX836E8AwAA // 8DAFBLAQItABQABgAIAAAAIQC2gziS / gAAAOEBAAATAAAA AAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If / WAAAA lAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAOGhBudDAgAA UwQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAIHnVGPg AAAACwEAAA8AAAAAAAAAAAAAAAAAnQQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACq BQAAAAA = "strokecolor =" бяло [3212] ">
Фигура 9.45 - Изчисляването на статично неопределен лъч
. При определяне на деформация на т Б от разпределен товар Q психически въведе допълнителна дозировка (виж фигура 8.45, б ..):
На деформация на края на конзолата мощност е равна на (виж Фигура 8.45 в ..):
Въз основа на условията (8.63), което се равнява изрази (8.64) и (8.65) за отклонение на лъча в т В .:
Намиране. Ние получи статично определен лъч, зарежда напречна интензитет разпределен товар р и има определена сила (реакция) (фиг. 8.45 гр). За да се конструира тази диаграма лъч и М (фиг. 8.45 г. W). преброяване на Х координата на десния край на М лъч. В.
отложи получени координати на ЕП. и да ги свърже с права линия - линейна зависимост ЕП. (Вж. Фиг. 8.45, д).
Както може да се види от израза за. огъващ момент диаграма съответства на квадратното парабола по отношение на координатната х. Две от ордината си в Другари А. Както вече дефинирани. За да намерите ордината ЕП. М в участък, където. изпълнява допълнителни изчисления.
От условието получаваме крайности на функция M:
Секционните греди имат екстремум на функцията на М в участъка на светлина:
Полученото уволни по ордината еп. Когато М (вж. Фиг. 8.45 гр).
Пример 9.9.2. За лъч, който се захваща от двете страни (фиг. 8.46, а) и е огънат от концентриран сила Р. разкрие статичен несигурност и да се изгради и диаграми.
Както бе споменато по-горе, счита лъч два пъти статично неопределен: неизвестни реакции - четири. и статични условия - две.
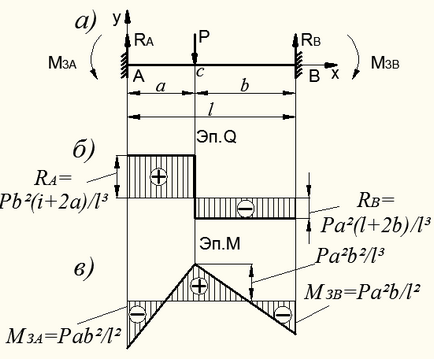
Фигура 8.46 - Изчисляването на статично неопределен лъч
От статични условия, ние имаме:
Предвид това, че ъгълът на въртене и извиване на носещата част Ь са равни на нула, ние получаваме две уравнения за определяне липсват реакции - условия щам съвместимост:
Решаването на получените уравнения (8.67) и (8.68) намираме реакцията:
Сега е лесно да се изгради схеми на срязващи сили и огъващи моменти. За тази цел ние изчисляваме огъващият момент в раздел В, под сила F:
Схеми и е показано на фиг. 8.46, б. инча
8.10.2. Непрекъснатото мулти-напречник
Непрекъснат, мулти нар греди, които имат повече от един полет. Те са статично неопределени и тяхното разкриване на излишък е удобно да се приложи методът на три момента уравнения. Един много прост пример, помислете за същността на този метод.
Пример 9.3. За лъч (фиг. 8.47, а) с изключение на балансьор лагери в краищата има междинен поддържащ. Неизвестните при изчисляването на огъване тези греди са три реакции на опорите и статични условия - две. Ето защо, този лъч ще веднъж статично неопределени.
Оповестяването на излишък от теоремата на три точки за допълнително неизвестното получава референтни точки М на междинен поддържащ 2. В рязане главата й и разделяне на светлина в две един участък (ris.8.47 б), тези моменти се определя от условията на съвместимост на щамове:
където - ъгъла на завъртане на правото подкрепа раздел 2 на единичен сноп между подпорите 1 и 2;
- ъгъл на завъртане на ляво подкрепа раздел 2 на единичен сноп между опорите 2 и 3.
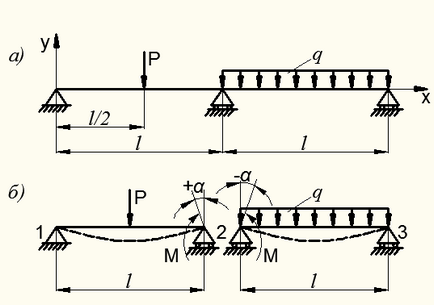
Фигура 8.47 - Изчисляване на два участъка греда, от теорема три _momentov
Тези ъгли на въртене на базата на правилата на знаци (.. Вижте Фигура 8.47, б) са изразени чрез външен товар и референтни точки:
Въз основа на изрази (8.72) и (8.73) с (8.71) получаваме уравнение за определяне на неизвестен излишни M:
След намирането на неизвестно допълнително полет всеки лъч се разглежда като статично определими греди натоварени с изключение на външен товар, има някои референтни моменти.
разкриване Метод статичен неопределеност multispan греди теоремата на три минути наречен така, защото, когато произволен брой светлини пунктове във всяка уравнение на тип съвместимост ъглови деформации (8.74) няма да включва повече от три опорни точки за разглеждане тата междинен поддържащ под типа състояние (8.71).
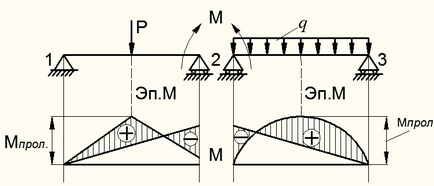
Изчисляване на огъване елементи всеки период след определяне съкратени неизвестни като статично определен лъч се произвежда чрез смесване (сумиране) на огъване елемент от външната натоварване и транзита вече определени референтни точки. Така, в този пример, полученият огъващ момент схема за всеки период на лъча. получен чрез наслагване ЕР. от предварително определен товар в летяща ЕП. на референтни точки
За горния пример е показано защрихованата на фиг. 8.48:
За първи полет. за второто преминаване. Така наслагване реакция определя върху опори и ЕР е конструирана. ,
Фигура 8.48 - Изграждане на огъване метод момент наслагване