Нормално разпределение в ексел
Рейтинг: 5/5
Нормално закон - основа и вследствие на много статистически методи. Но не заради факта, че първоначалните данни са нормално разпределени, това не е така, но тъй като има по-силна причина - централната лимит теорема. Следователно, нормално закона се използва много по-често, отколкото се среща в природата.
Математически нормален закон е функция, с която вероятността за намиране на променлива от дадените стойности. Тя може да бъде, и обратно, се изчислява стойността на променливата на тези вероятности. Това ще изисква обратна функция на нормалното разпределение. В ума, в сметките, или дори калкулатор за извършване на тези изчисления създаде много проблеми, така че има специални таблици. Между другото, най-добрата колекция на статистически таблици са в bibliotechke.
Използвайте маси е доказал себе си добре, но има по-ефективен начин за изчисляване на вероятността. Това Excel, която предвижда специални функции за обработка на нормално разпределени данни. Има няколко от тях.
Както е известно, на нормално разпределение N (ц, σ 2) зависи от два параметъра: очакване (μ) и отклонение (σ 2). Стандартният нормално разпределение, те съответно са 0 и 1, т.е. N (0, 1). Той е създаден за маса нормализира данни споменато по-горе.
След това ще се съсредоточим върху Excel функции (по-долу формули, да не се бърка с функции за разпространение), можете да използвате, за да автоматизирате (т.е. хиляда пъти, за да се ускори) процеса на намиране на вероятности.
функция NORM.ST.RASP
NORM.ST.RASP формула се използва за изчисляване на плътността на φ (Z) или вероятността от φ (Z) на нормализираните данни (Z). В синтаксиса на следната формула.
Z - стандартизирана стойност на променливата
Integral - ако 0 изчислява φ плътност (Z). ако 1 - стойност на функцията F (Z), т.е. вероятността P (Z Превод на български език на последното поле, разбира се, загаси лампата. И се изчислява стойността на функция плътност за всеки Z: -3, -2, -1, 0, 1, 2, 3 (което ние говорим в клетка А2). За да се изчисли необходимото плътност = NORM.ST.RASP формула (А2 0). Графиката по-долу - това е червена точка. За изчисляване на стойностите на NORM.ST.RASP = (А2; 1). На диаграмата по - сенчести площ под кривата на нормалното. В действителност често се налага да разчита на вероятността, че случайна стойност няма да надхвърля определени граници от средната стойност (в стандартното отклонение, отговаряща на променливата Z), т.е. P (| Z | Определете каква е вероятността за случайна променлива, попадащи в рамките на ± 1 z, ± 2z и 3z ± нула. За това е необходимо да се използва една от характеристиките на всеки непрекъснат разпределение и вземе разликата: F (Z) -F (-Z), или получаване на същия резултат, 2F (Z) -1. В Excel ще изглежда както следва: = 2 * NORM.ST.RASP (А2; 1) -1. Диаграмата ясно видими основните свойства на нормалното разпределение, включително три правило сигма. според която в рамките на ± 3 стандартни отклонения от средните стойности почти всички затворени. То може да бъде обратен проблема: от съществуващата вероятност P (Z NORM.ST.OBR формула изчислява обратна на стандартното нормално разпределение. Синтаксисът се състои от един параметър: вероятност - вероятността. Тази формула може да се използва толкова често, колкото предишния, защото в същите таблици трябва да изглежда не само вероятно, но квантил (тези на Z, съответстващи на дадена вероятност). Действителното прехвърляне на задачи обикновено се различават и трябва да се използва всеки дизайн с тази формула. Уместно е да се припомни, доверителните интервали. което зависи от нивото на доверие. Това е отклонение от средната стойност, но този път на определена вероятност и стойност Z изчисленото.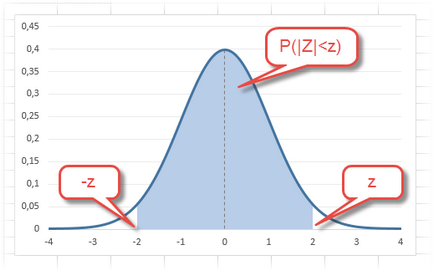
функция NORM.ST.OBR
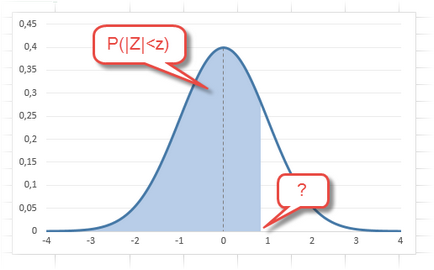
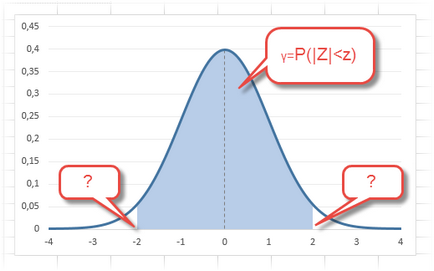
Като се има предвид, че доверителния интервал се състои от горна и долна граници, и че нормалното разпределение е симетричен по отношение на нула, достатъчно е да се изчисли горната граница (положително отклонение). Долна граница се взема с обратен знак. Означаваме вероятността на доверие като γ (гама), след това поносимостта се изчислява по следната формула
Сега се изчисли стойности Z (който съответства на отклонението от средната стойност в Sigma) в продължение на няколко вероятности, включително тези, които са известни от сърцето всички статистически данни, т.е. доверителни интервали за вероятността от 90%, 95% и 99%. В клетка В2 ние говорим формулата: NORM.ST.OBR = ((1 + А2) / 2). Чрез промяна на стойността на променливата величина (вероятност в клетка А2) се получат различни интервали граница.
Както се вижда доверителен интервал 95% е 1,96, което е почти две стандартни отклонения. Оттук и възможното разпространение на нормална случайна променлива по-скоро лесно дори и в оценка ум (например, средно аритметично, които по силата на централната лимит теорема има нормално разпределение). Като цяло, при ниво на доверие 90%, 95% и 99% доверителни интервали съответства на ± 1.64, 1.96 ± и ± 2,58 σ.
Общо NORM.ST.RASP и NORM.ST.OBR функции позволяват да се правят изчисления, свързани с нормално разпределение. Но, за да се улесни и да се намали броят на действия на Excel, има няколко други функции. Например, за изчисляване на доверителни интервали от средната стойност може да се използва DOVERIT.NORM. За да тествате статистически хипотези за средното аритметично е формула Z.TEST. Но отново, можете да направите, без да ги ако използвате структурата на горните формули.
Помислете за няколко примери за полезни формули.
функция NORM.RASP
функция NORM.RASP различава от NORM.ST.RASP само с това, че се използва за обработка на данни от всякакъв размер, а не само стандартизирана. нормални параметри за дистрибуция са посочени в синтаксиса.
Средната - очакването да се използва като първи параметър на нормален модел на разпределение
standard_dev - стандартно отклонение - втори модел параметър
Integral - ако 0, тогава плътност се изчислява, ако 1 - стойността на функцията, т.е. P (X Например, за да се изчисли стойността на плътността на 15 се отстранява от нормална проба с математически очакване на 10, стандартно отклонение от 3 до напиши следната формула: Ако последният вариант е да се сложи 1, а след това ние получаваме вероятността нормална случайна променлива ще бъде по-малко от 15 за дадените параметри на разпределение. Следователно, вероятността да се изчислява директно от първоначалните данни. Това е обратна функция на нормалното разпределение. Синтаксисът е както следва. вероятност - вероятност standard_dev - стандартно отклонение Определения са същите няма да се повтори. Присвояване на същата като тази на NORM.ST.OBR, само тази функция работи с данни от всякакъв мащаб, които, разбира се, във формулата показват параметрите на нормалната закона. Един пример е показан на видеото в края. Функциите, описани по-горе, много да облекчи живота и да спести време. Но най-малкото което можете да направите, без тях, защото има статистически таблици. Но понякога, без формули по никакъв начин. Един пример е генерирането на случайни числа. В Excel, има две функции, които дават случайни числа. Първият от тях RANDBETWEEN. Тя извежда случайни числа, равномерно разпределена в определените граници. Можете, например, на случаен принцип избере победителите от конкурса или да създадете парола. Втората функция на RAND генерира равномерно разпределени случайно число между 0 и 1. Това е е необходимо тази функция, за да се изкуствен проба с определена разпределение (не само нормално). RAND ще генерира случайна вероятност, които също имат граници от 0 до 1. описание с помощта на обратна функция на нормално разпределение (стандарт или конвенционален) се превръща в нормални номера. Да приемем за експеримента трябва да получи проба от нормално разпределение с математическо очакване от общото население на 10 и стандартно отклонение 3. За един-единствен запис формула случайна стойност Преместете го до желания брой клетки и нормалната проба е готова. За симулиране на стандартизирани данни трябва да се използват NORM.ST.OBR. Процесът на преобразуване е еднакъв в нормални номера може визуално изобразяват от следната таблица. От еднаквото вероятността, които са генерирани от формула RAND, да хоризонтална линия на графиката на функцията за нормално разпределение. След това вероятностите на точките на пресичане с графиката пропуснати проекция върху хоризонталната ос.функция NORM.OBR
Нормално генератор на случайни числа
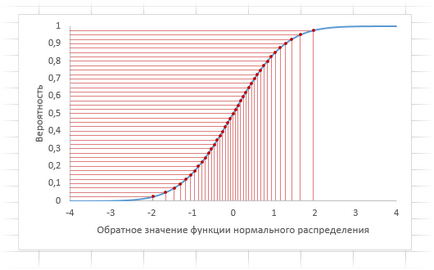
На изхода стойностите, получени с типична концентрация в близост до центъра. Това е връщане минава през нормалната функция на разпределение на броя на навивките в нормална униформа. Excel ви позволява да играете неограничен брой проби от всякакъв размер в рамките на няколко секунди.
Както обикновено, придружаващата видеото, където всички по-горе е показана в действие.