Намираме уравнението на линейна регресия параметри и дават коефициент икономическа интерпретация

1. Намерете параметрите на уравнението на линейната регресия, за да се даде икономическа интерпретация на коефициента на регресия.

2. Изчисляване на остатъците; намерите остатъчната сума от квадрати; Оценка на остатъците дисперсията; парцел на остатъците.

3. Проверка на изпълнението на предположенията МНМК.

4. Извършва от значението на параметрите на регресия уравнение, използвайки т-тест на Student (# 945 = 0.05).

5. Изчислява се коефициентът на определяне, тест значението на регресия уравнение, използвайки F - критерий на Fisher (# 945 = 0.05), за да намери средната относителна грешка на приближение. За да се направи заключение за качеството на модела.

6. Прилагане предсказване Y Средната стойност на индикатора при ниво на значимост # 945; = 0.1, ако предвидената стойност на фактор X е 80% от максималната си стойност.

7. Осигуряване на графичен модел и действителната стойност Y предсказание точка.

8. Напишете уравненията на нелинейна регресия и изграждане на графиците си:

9. За тези модели, за да намерите най-Коефициентите за установяване и средна относителна грешка на приближение. Сравнете моделите на тези характеристики и да се направи заключение.

Ние считаме, параметрите на уравнението на линейна регресия и да даде икономическа интерпретация коефициент регресия.

Линеен регресионен уравнение има следния вид:

Изчисленията за намиране на параметри А и В са дадени в Таблица 2.

Стойностите, изчислени за намиране на параметрите на уравнението на линейна регресия.

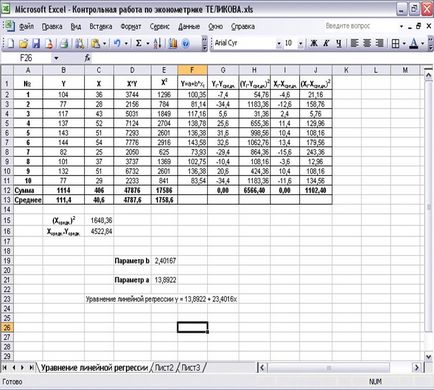
уравнението на регресия е: у = 13,8951 + 2,4016 * х.

С увеличаването на инвестициите обем (X) до 1 млн. Разтрийте. обем на изход (Y) ще се увеличи със средно 2,401,600 рубли .. По този начин, има данни за положителна корелация, което показва, че ефективността на предприятията и рентабилността на инвестициите в тяхната дейност.

2. Изчисляване на остатъците; намерите остатъчната сума от квадрати; Ние изграждане на вариацията оценяват ostatkovi графиката остатъци.

Остатъчната сумата от квадратите на отклоненията: = 207.74.

Дисперсионни остатъци: 25.97.

Изчисленията са показани в таблица 3.

остатъци графика има формата:

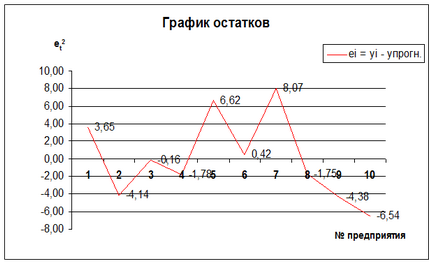
Фиг.1. остатъци График

3. Проверете дали МНК предпоставки, който включва елементи:

- проверка на равенство на очакването на случаен компонент на нула;

- случаен характер на остатъци;

- съответствие с редица останки от нормален закон за разпределение.

Проверка на равнопоставеността на нивата на очакванията на редица баланси на нула.

Извършва се по време на одита, съответстваща нулевата хипотеза H0:. За тази цел построена тениски статистика. къде.

. По този начин, хипотезата е приет.

На случаен характер на остатъци.

Ние ще провери броя на случайни нива на остатъци чрез завъртане критерии точки:

Броят на повратни точки се определя от таблицата с остатъци:

= 6> [4,3029], следователно, собственост на случайността остатъци изпълнена.

Независимост на остатъци се проверява с помощта на тест Durbin - Watson:

Тъй като падна в диапазона от d2 до 2, а след това този критерий може да се заключи за изпълнението на имоти за независимост. Това означава, че броят на високоговорителите не съществува автокорелация, така че моделът е адекватен на този критерий.

Стойност серия остатъци нормално разпределение се определя с използване на R / S-критерии за критичните нива (2.7-3.7);

Ние се изчисли стойността на RS:

където Emax - максимален брой нива на остатъчен Е (т) = 8,07;

Emin - минимален брой нива остатъци Е (т) = -6,54.

S - стандартно отклонение = 4,8044.

От 2.7<3,04<3,7, и полученное значение RS попало в за-данный интервал, значит, выполняется свойство нормальности распределения.

По този начин, като се има предвид различните критерии за изпълнение оли предположения стигнали до извода, че са изпълнени предпоставките OLS.

4. да се провери значението на параметрите на регресионно уравнение с помощта на Т-тест на Стюдънт # 945; = 0,05.

Тестване на важността на отделни регресионни коефициенти, свързани с определянето на Т-тест изчислени стойности (т-статистики) за съответните регресионни коефициенти:

След това, изчислените стойности се сравняват с табличен ttabl = 2,3060. Таблично стойност критерий определя от (N 2) степени на свобода (п - брой наблюдения), и съответното ниво на значимост а (0,05)

Ако изчислената стойност на т-тест с (п-2), неговата бодове градуси по-голяма от неговата маса стойност на дадено ниво znĂ-chimosti, коефициент на регресия се счита за значително.

В този случай, коефициенти на регресия A0 - незначителен, A1 - значимите коефициенти.

5. изчисли коефициентът на изчисление, проверява значението на регресионно уравнение с pomoschyu- критерий на Фишер, ние откриваме, средна относителна грешка на приближение. За да се направят изводи за качеството на модела.

Ние дефинираме линеен коефициент на двойката корелация съгласно формула

Ние изчисляваме коефициентът на изчисление:

Тя показва изменението на ефективно фракция на функция, под влиянието на изследваните фактори, т.е. Той определя каква част от вариацията на Y се взема предвид в модела и се дължи на влиянието на фактори върху него.

Колкото по-близо R 2: 1, по-добро качество на модела.

Вариант доведе Y (обем изход) на 96.8% обяснено вариант фактор X (обем раширения главни букви).

Оценка на значимостта на регресионно уравнение за провеждане Pomo-schyu Fisher F-тест:

Уравнението на регресия с вероятност 0.95 цяло Статис имат възможност за значително, т.е.. за. F> Ftabl.

Ние определяме средния относителен сближаване грешка:

средните изчислени стойности за у-линеен модел на действителните стойности се различават от 3.863% до

Тъй като грешката сближаване на модела е по-малко от 7%, това показва добра като модел.

6. Ние извършваме предсказание средно pokazatelyapri степен на значимост, ако предвиденото стойността на фактора Hsostavit 80% от максималната си стойност.

Прогнозна стойност на индекса, ако предвидената стойност на фактор X е 80% от максималната си стойност от 0.8 * 54,00 = 43,20, ще бъде:

Y е предаване = 13,89 + 2,40 * 43,20 = 117,64.

за степените на свобода и ниво на значимост от 0.1 е равно на 1.8595.