Линейни алгоритми - диаграма структура и изчисление

В ежедневието на всеки човек е да се справят с огромен брой задачи с различна трудност по време на работа или по време на следването. Някои задачи са толкова прости, че в тяхното изпълнение, което правим определени действия автоматично, без дори да се замисли. Решението на всеки проблем, дори и най-простите, като правило, се провежда последователно в продължение на няколко стъпки. Този вид последователност в решаването на проблеми, се нарича алгоритъм. Днес ние погледнете какво линейно алгоритми, тяхната структура е представен като взели решение и програмиране.

алгоритмичен език

Тази концепция е точната рецепта за художника да направи поредица от действия, които се насочват към решаването на проблема.

Този език е средство за описване на алгоритми, които са насочени най-общо на потребителя.

Говорейки в компютърен език, както е посочено от точната рецепта, определяне на изчислителните процеси. Той, от своя страна, води от първоначалните данни, че гама, към първоначалния резултат.

Разработване на алгоритъм - е доста сложно и отнема много време процес. Тя представлява съвкупност от техники (развитие на) последователност от действия, предназначени да се справи с проблемите, с помощта на компютри.

свойства алгоритъм

Сред свойства излъчват:

• крайник - е завършването на целия алгоритъм за определяне на краен брой стъпки (стъпки);
• сигурност (недвусмислено) - представлява уникалността на правила за тълкуване за извършване на действия, както и реда на тяхното изпълнение;
• ефективност - желаните резултати за всеки краен брой стъпки;
• ясни - ясни инструкции трябва да бъдат изпълнителя;
• масовите - алгоритми трябва да могат да се реши даден клас проблеми, специфични за широката формулировка на проблема.

Линейни алгоритми. Компютърен клас 9

Вече обсъдихме определението и характеристиките на концепцията. Сега нека да поговорим за нейните форми:

Ние сме заинтересовани от линейни алгоритми. Кои са те? Те съдържат команди, за да се изпълняват една след друга в ясна последователност.

В линейната структура на алгоритъма може да се запише в устна и графичен вид.

Ето един пример, записана в устна форма. Така, задачата: Събирайте училище. решение:

Графично форма predsatvlyat горе процес ще бъде както следва:

Линеен алгоритъм под формата блокова схема,

Блоковата схема представлява примерен алгоритъм изображение, в което всяка отделна фаза е представено от блокове представени в различни геометрични форми. Освен това, връзката между етапите (с други думи, последователността на фаза изпълнение) е показано със стрелките, които свързват парчета (блокове). Всеки блок е придружен от надпис. За типични действия следните геометрични форми се използват в линеен алгоритъм:

• Блок старт в края на алгоритъм. На блока е надпис "начало" или "края".
• "Вход-изход" единица. Този блок се под формата на успоредник. Той постави следния надпис: "Input", "отнемане", "печат". Също така, прикрепен към тях списък на входа или, съответно, на изходните променливи.
• Аритметика елемент или каре решения. Тя отговаря на правоъгълник. Дисплеят трябва да бъде: "работа", "група от операции."

Но с помощта на блок-схеми, изобразен разтвор на линейни алгоритми. На следващо място, нека да говорим за функциите на възлагане на ценности.

Линейни алгоритми за изчисление

Главна елементарни действия в изчислителни алгоритми - тази задача на променливите определена стойност. В случая, когато константата определя от формата на неговата запис, получават специфична променлива стойност единствено като резултат на заданието. Това може да се извърши по два метода: чрез инструкция задача; чрез въвеждане на команди.

Един пример на алгоритъм за решаване на линейни

• числител на фракцията 1 трябва да бъде умножена по знаменател от фракция 2;
• 1 знаменателя да бъде умножена по числителя 2;
• искате да запишете дроб, чийто числител е резултат от прилагането на параграф 1, а знаменателят - резултат от 2 точки. Алгебрична форма на това правило е, както следва:

Така че, ние изграждаме компютърен алгоритъм за разделяне на фракции. За да се избегне объркване, ние ще използваме за променливите са същите значения, както във формулата, която е била посочена по-горе. а, б, в, d-оригиналните данни като цели числа. Резултатът ще бъде целочислени стойности. разтвор алгоритмичен език ще бъде, както следва:

SAL разделяне на фракции

Графични решения формат

Схема линеен алгоритъм, описани по-горе, е както следва:

присвоява стойност на екипа има следния формат:

Знакът "=" се чете като целеви.

Задание - екип, който е необходим за компютър, за да изпълните следните действия:

• оценка на експресията;
• определяне променливи стойности, получени.

По-горе алгоритъм има две команди като задача. В блок-схема на задача команда трябва да бъде записана в правоъгълник, който се нарича изчислителния блок.

Когато е описано от линейни алгоритми, няма особена нужда от задължително спазване на строги правила при писане изрази. Можете да ги записвате с помощта на обичайните математическа форма. Но това не е строг синтаксис език за програмиране.

В този пример, алгоритъмът също влезе в екипа:

вход команда в графиката е на успоредник, т.е. входно-изходното устройство. При изпълнение на тази команда, процесорът прекъсва, докато потребителят ще извърши определени действия. А именно, потребителят трябва да входно устройство (клавиатура) тип входни променливи (техните стойности) и натиснете Enter, която действа като ключ Enter. Важно е, че стойностите са били въведени в същия ред, като списъкът на входа, който се намира в съответните променливи.

Linear алгоритъм. неговото програмиране

Както бе споменато по-рано в тази статия, линейната програма може да включва подобни изказвания:

Това означава, че с помощта на горните оператори да линейното програмиране алгоритми.

По този начин, операторът за присвояване в езика за програмиране е написано, както следва:

LET А = В, където А - променливата В - експресия. Например, А = Y + 20.

влизане оператор е както следва:

INPUT, например: INPUT С

изходните данни на оператора, стойностите написани във формата:

Печат. Например S. ПЕЧАТ

Ето един прост пример. Ние трябва да се напише програма, която ще намерите в размер на вход от клавиатурата числа А и Б.

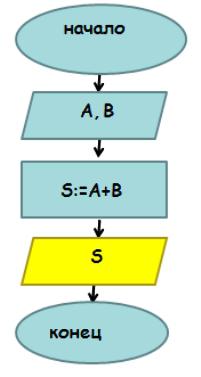
Програмен език, ние получаваме една програма, текстът на която е показано по-долу.

оператори за навлизане, изход в езика за програмиране Pascal

Паскал не разпределя специални оператори, което показва операциите, входящите или изходящите които използват линейни алгоритми. Програмите за обмен на информация се осъществява с помощта на вградени процедури. Тъй като няма нужда от предварително описание на стандартната процедура, тя е на разположение за всяка програма, съдържаща позоваване на него. Също така на името на въпросната процедура, не проектира всяка ключова дума.

При въвеждане на данни с помощта на тези оператори за достъп до стандартната процедура на въвеждане на данни, който вече е интегриран в програмата.

Прочетете (A, B, C), където A, B, C - променливи, които трябва да бъдат въведени в паметта за съхранение.

Readlnn (x1, Y, x2) - попълване на влизане, курсорът скача до началото на нов ред.

Readlnn; - показва, че чака натиснете «Влез». Обикновено този оператор се вмъква в текста преди крайния «Край», за да запазите резултатите от програмата на съдържанието на екрана.

Изходни данни за екрана на монитора с помощта на тези оператори:

Напишете (A, B, C) - определяне на стойностите на A, B, C в един ред, а курсорът не оставя на текущия ред.

Writeln (Z, Y, z2) - завършва изходните стойности, курсорът ще се премести в нов ред в тази позиция.

writeln; - свидетелства за да премине линията и да се премести в началото на нова.

Но с помощта на такива прости твърдения и извършва вход и изход на данни в Паскал.