Как да се изчисли коефициента на корелация се отличи, exceltip
В днешната статия ще се фокусира върху това как променливи могат да бъдат свързани един с друг. С помощта на корелация, ние може да се определи дали има връзка между първата и втората променлива. Надявам се, че този урок ще намерите не по-малко вълнуващо от предишните!
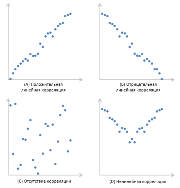
Съотношение измерва силата и посоката на връзката между х и у. Фигурата показва различните видове корелация като разсейване на наредени двойки (х, у). Традиционно, променливата х е разположен на хоризонталната ос и у - вертикална.
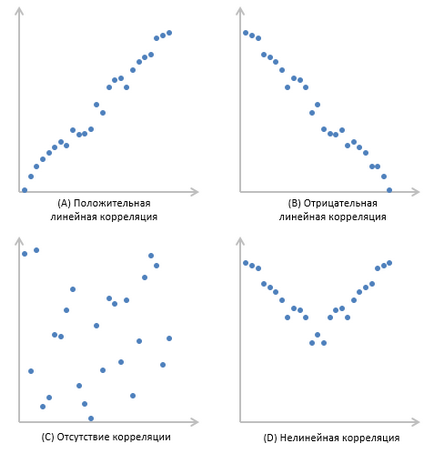
Графика А показва пример за положителна линейна корелация: увеличаването х също се увеличава, и линейно. Графика В ни показва пример на отрицателно линейна корелация където х нараства линейно от намалява. В графиката може да се види с липсата на корелация между х и у. Тези променливи не влияят един на друг.
Накрая, графика D - е пример за нелинейни взаимоотношения между променливи. С увеличаване х в първите намалява, а след това променя посоката и се увеличава.
Останалата част от статията е посветена на линейна връзка между зависими и независими променливи.
коефициент на корелация
Коефициентът на корелация, R, ни предоставя както на силата и посоката на връзката между независими и зависими променливи. Стойностите на R са в границите между - 1,0 и 1,0 +. Когато R е положителен, връзката между X и Y е положително (таблица А на фигурата), и когато стойността на г е отрицателна, и отрицателна връзка (таблица В). Корелационният коефициент е близо до нула, това показва, че съществува графиката С) между х и у връзки.
Якостта на връзката между X и Y се определя от близост до коефициент на корелация - 1.0 + или - 1.0. Разглеждане на следващата фигура.
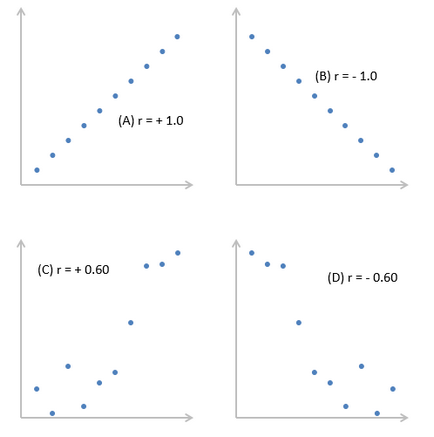
Графика А показва идеално положителна корелация между х и у, когато R = + 1.0. Схема Б - идеално негативна корелация между х и у, когато R = - 1,0. Графики С и D - примери слабите връзки между зависими и независими променливи.
Корелационният коефициент, R, както определя силата и посоката на връзката между зависими и независими променливи. R стойности, вариращи от - 1.0 (силна негативна корелация) до 1.0 + (силна положителна корелация). За г = 0 между променливите х и у, няма връзка.
Ние можем да се изчисли реалната корелационен коефициент се използва следното уравнение:
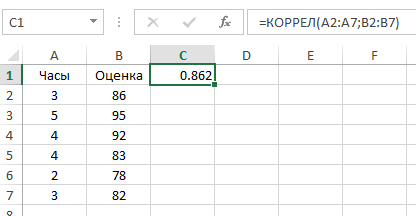
Е, добре! Знам, че изглежда ужасно уравнение като смесица от неразбираеми символи, но преди да се удрят в паника, нека да го прилага по отношение на примера на резултатите от тестовете. Да речем, че искам да се определи дали има връзка между броя на часовете, посветени на студентските учи статистика и финален изпит клас. Таблицата по-долу ще ни помогне да се прекъсне това уравнение с няколко прости изчисления и да ги направи по-лесно управляеми.
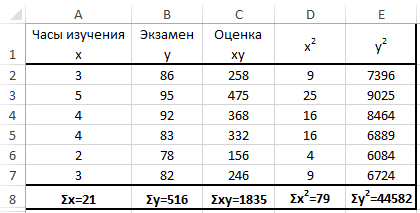
Както можете да видите, между броя на часовете, посветени на изучаването на този въпрос, и разглеждането води там е много силна положителна корелация. Учителите ще бъдат много щастливи да знаят за това.
Каква е ползата да се установи връзка между тези променливи? Добър въпрос. Ако се установи, че е налице връзка, ние можем да се предскаже резултатите от проверката въз основа на определен брой часове, посветени на изучаването на този въпрос. Казано по-просто, по-силна е връзката, толкова по-точни ще бъде нашата прогноза.
Използване на Excel за изчисляване на коефициентите на корелация
Сигурен съм, че като погледнете в тези ужасни корелационните коефициенти на изчисление, ще изпитате истинска радост да се научат, че програмата Excel може да изпълнява за вас цялата тази работа с помощта на функцията CORREL със следните характеристики:
CORREL (гама 1, гама 2)
масив = 1 данни варират за първата променлива,
масив 2 = данни диапазон за втората променлива.
Например, фигура показва функция CORREL използвани при изчисляването на коефициента на корелация за примера на оценката на изпит.
Може би ще се интересуват от следните статии
Разбира се, всичко е описано и на разположение по темата. Какво иска той. Аз трябваше да покаже зависимостта на продажбите на магазините на времето. Всичко се оказа и това е съвсем логично.
Ние трябва да погледнем и др. Член, надявам се да намеря нещо друго полезно.
Благодаря.
Благодаря ви, много ясно.
Можете цитират като пример за изчисляване на съотношението на персонала, т.е. до размера на тези променливи (напр. С часове и оценка). Prompt и къде да се отличи функция ANOVA или МАНОВА - Ной изчисляване на отношенията съотношение между качеството и количеството на тези променливи?
Добър ден! Как да се изчисли съотношението в excele разбрах. Няколко изясняващи въпроси. Първо, тъй като тя се изчислява КР. Pearson? И второто. Калкулационните които изчисляват ядро. Pearson корелация със стойността, посочена също «р» (обикновено p0,05 или 0.01), и по excele той какво? И третия. Ако формулата за изчисляване на Пиърсън навсякъде едно, защо различни калкулатори, включително и в сравнение с изчисленията в excele, получени различни резултати? Що се отнася до "P" - друго искане: Аз съм приятел с малко matimaitkoy, а не приятели с статистика на всички. Мога ли да обясни на достъпен език за тази област?