Кубични уравнения са на формуляра ос 3 + 2 + BX СХ + г = 0. Метод за решаване на тези уравнения е известно за няколко столетия (тя е била открита в италиански математиците 16 век). Решите няколко кубични уравнения е доста трудно, но с правилният подход (и добро ниво на теоретични познания), вие ще бъдете в състояние да реши дори най-трудните кубични уравнения.
стъпки Редактиране
Метод 1 от 3:
Решението по формулата за решаване на квадратно уравнение Редактиране
Проверете дали можете да представлява кубически уравнение постоянен мандат. Както бе споменато по-горе, кубични уравнения са с форма ос на 3 + BX 2 + СХ + г = 0, където коефициентите "б", "в" и "г" може да бъде равно на 0, т.е. кубичната формула може да се състои от само един член (ове променлива в трета степен). Първо проверете дали сте представи кубически уравнение постоянен срок, тоест, "г". Ако има свободен член, можете да се реши този кубически уравнение с помощта на формулата за решаване на квадратно уравнение.
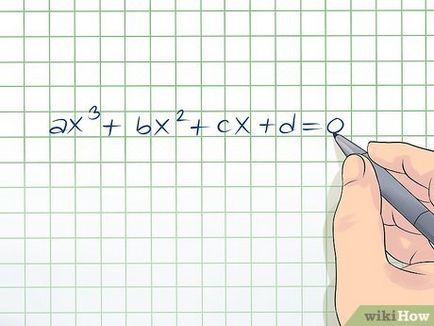
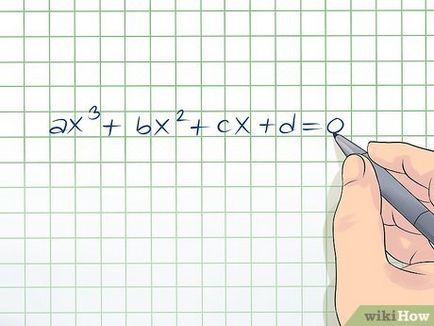
- Ако свободен член там, да се използва друг метод на разтвор (виж следващия раздел).
Тъй като в това уравнение не е свободен термин, всички членове на това уравнение съдържа променливата "х", които могат да бъдат извадени от скобите: X (брадва 2 + BX + в).
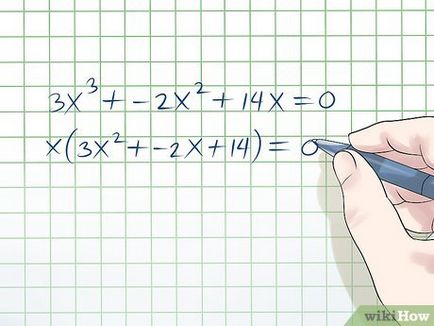
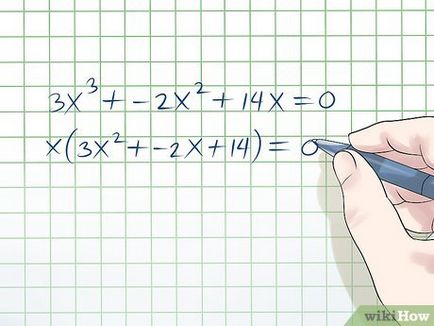
- Пример. 3x 3 + 2 + -2x 14ч = 0. Ако се направи "х" на конзолите, получавате х (3x 2 + -2x + 14) = 0.
Имайте предвид, че уравнението в скоби - това квадратно уравнение на формуляра брадва 2 + BX + С, което може да бъде решен с помощта на формула (Ь +/- √ (б 2 - 4ав)> / 2а). Решете квадратно уравнение и да решите кубичен уравнението.
- В нашия пример, да бъде заменен стойности на коефициентите "а", "б", "C" (3, 2, 14) във формулата: б +/- √ (б 2 - 4ав)> / 2а / 2 (3) / 6 / 6/6
- Разтвор 1: / 6 I> / 6
- Разтвор 2: I> / 6
Не забравяйте, че квадратно уравнение има две решения, куб - три решения. Тук ще намерите две решения на площада, и, следователно, на кубичен уравнението. При изваждане на "Х" на конзолите, третото решение е винаги 0.
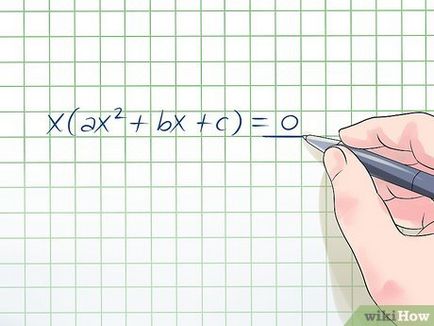
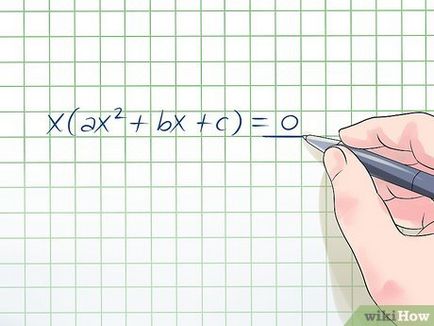
- Това е вярно, тъй като всяко число или израз, умножено по 0 е 0. Така че сте взели от "Х" на конзолите, вие се разпространява един кубичен уравнението на два фактора ( "Х" и квадратно уравнение), единият от които трябва да бъде равна 0, така че цялата уравнението е 0.
Метод 2 на 3:
Намирането на цялостни решения, използващи факторинг Редактиране
Проверете дали можете да представлява кубически уравнение постоянен мандат. Описани в предишния раздел, методът не е подходящ за решаване на кубични уравнения, в което свободното Терминът присъства. В този случай, ще трябва да се използва метода, който е описан в тази и следващите раздели.
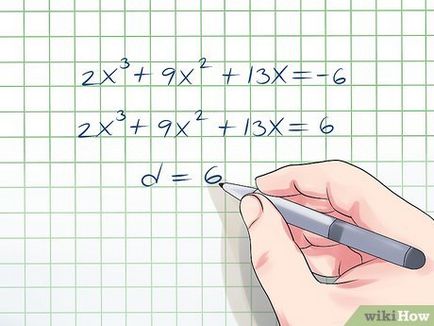
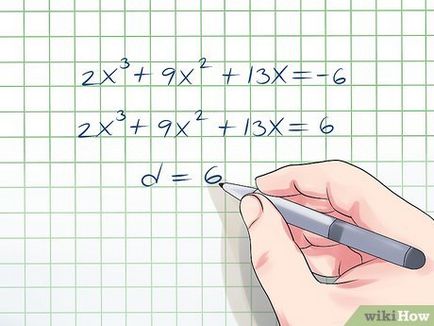
- Пример. 2x 3 + 2 + 9х 13x = -6. Ето прехвърляте член свободен г = -6 към лявата страна на уравнението, за да получите от дясната страна 0: 2x 3 + 9x 2 + 13x + 6 = 0.
Коефициент множители получат "а" (коефициент на 3 х) и постоянен мандат "D". Фактори на - число, което, когато се умножат, дават първоначалния брой. Например, броят на множители 6 са числата 1, 2, 3, 6 (1 * 6 = 6 и 2 х 3 = 6).
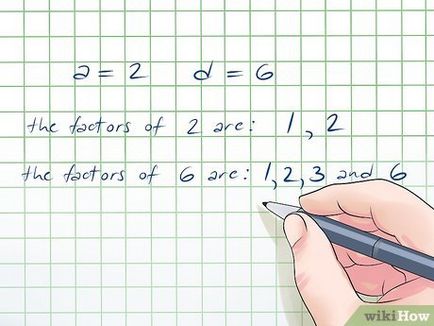
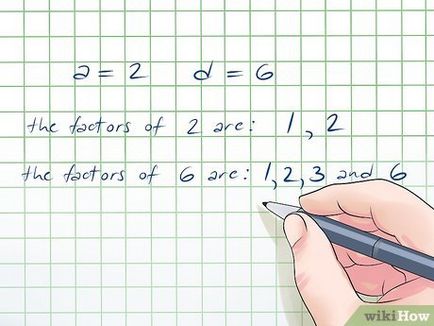
- В този пример, а = 2 и г = 6. мултипликатори 2 - е числото 1 и 2. мултипликатори 6 - е числото 1, 2, 3 и 6.
Разделете коефициент множители "и" В условията на свободен множители страни "D". Можете да получите фракции и числа. Цялото решение на квадратното уравнение, ще бъде или едно от тези числа, или отрицателна стойност на една от тези числа.
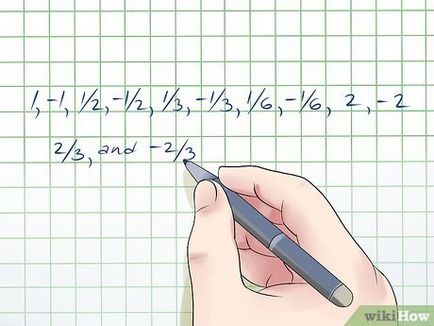
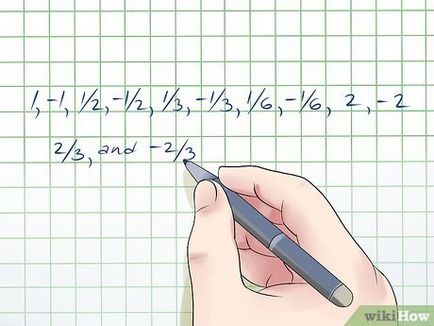
- В нашия пример, се разделят фактори "а" (1, 2) от фактори "D" на (1, 2, 3, 6) и получават: 1, 1/2, 1/3, 1/6, 2, 2/3. Сега се добавят към този диапазон от числа на отрицателни стойности са 1, 1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 , -2/3. Цели решения на квадратното уравнение, вие сте в тази поредица от числа.
Сега можете да намерите цялата си решения на кубичен уравнението, замествайки числата от набор числа намерен. Но ако не искате да губите време за това, моля използвайте разделение Хорнър схема. Тази схема се приема число разделяне на стойностите на "А", "В", "С", "г" на кубичен уравнението. Ако остатъкът е 0, цяло число е един разтвор на кубичен уравнение.
- схема дивизия Horner - трудна тема; за повече информация относно това, кликнете върху линка по-горе. Ето един пример за това как да се намери едно от решенията, дадени ви от квадратното уравнение, като се раздели схема Хорнър: -1 | 09 февруари, 13 г. Юни __ | -2-7-6 __ | 2 7 6 0 0 Както остатъкът, след едно от решенията е цяло число 1.
