Как да направите магически квадрат

Има няколко различни класификации на магически квадрати

петия ред, предназначен да ги организирате по някакъв начин. В книгата

броят на централния площад. Метод интересно, но не повече.

Колко шести порядък площади все още е неизвестен, но те са около 1,77 х 10 19 Брой огромен, така че няма никаква надежда да ги брои с помощта на изчерпателно търсене, но формулата за изчисляване на магически квадрати човек може да се сетиш.

Избрано много начини за изграждане на магически квадрати. Най-лесният начин да направите магически квадрати на нечетен ред. Ние използваме метода, който се предлага да се френския учен от XVII век от А. де ла Luber (De La Loubère). Тя се основава на пет правила, ефектът от които ще разгледаме много прост магически квадрат от 3 х 3 клетки.

Правило 1. Сложете 1 в средната колона на първия ред (фиг. 5.7).

Фиг. 5.7. Първият номер

Правило номер 2. След това място, ако е възможно в клетка, съседна на ток диагонално надясно и отгоре (фиг. 5.8).

Фиг. 5.8. Ние се опитваме да вкара втория номер

Правило 3: Ако новата клетка е извън квадратен върха. запише броя в най-долния ред и следващата колона (Фиг. 5.9).

Фиг. 5.9. Поставяме втория номер

Правило 4: Ако клетката е извън квадрата надясно. се записва броят на първата колона в предишния ред (фиг. 5.10).

Фиг. 5.10. Ставайки третото число

Правило 5. Ако клетката вече е заето. след друг запис номер за текущата клетка (фиг. 5.11).

Фиг. 5.11. Ние събрахме четвърти брой

На следващо място, се движат по член 2 (фиг. 5.12).

Фиг. 5.12. Сложете на пети и шести номер

Отново, следват инструкциите 3, 4, 5, не е изготвени целия квадрат (фиг.

Не ми ли е, правилата са много ясен и прост, но все пак досаден да организира дори 9-те числа. Въпреки това, знаейки, че алгоритъмът за изграждане на магически квадрати, ние можем лесно да прехвърлите на компютъра всичко рутинната работа, оставяйки си само творчески, която е да се напише програма.

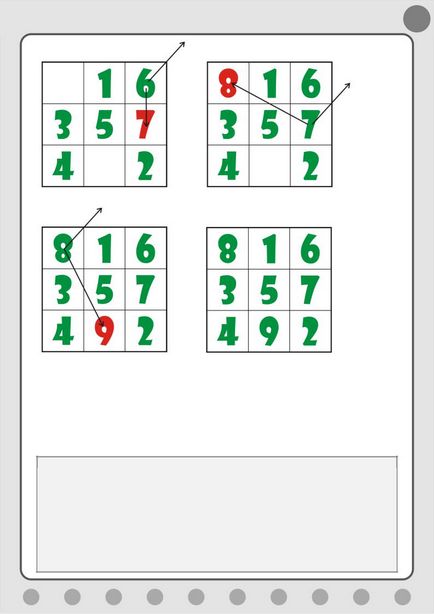
Фиг. 5.13. Напълнете квадрат следните номера

Проект магически квадрати (магия)

Задаване на полета за програмата магически квадрати е съвсем очевидно:

// ПРОГРАМА за генериране

// нечетен магически квадрати

// МЕТОД DE LA Lubero

публична частична клас Form1. форма

// макс. квадратен площ: конст Int MAX_SIZE = 27; // Var

Int п = 0; // цел на MQ квадратен Int [,]; // магически квадрат

Int номер = 0; // текущия брой записи на площада

Int колона = 0; // текущата колона Int ред = 0; // ток линия

Метод де ла Lubero подходящ за подготовката на нечетните площадите на всякакви размери, за да можем да предостави на потребителя възможността да избират реда на площада, е разумно, тъй като ограничава свободата на избор на 27-D клетки на.

След като потребителят кликне върху ценните btnGen Генериране на бутон. метод btnGen_Click създава масив за съхранение на номера и отива да генерира метод:

// натиснете "Generate"

частен невалидни btnGen_Click (обект подател, EventArgs д)

п = (междинно съединение) udNum.Value;

MQ = ново междинно съединение [п + 1, п + 1];

// Генериране магически квадрат: генериране ();

Тук ние започне да действа в съответствие с правилата де ла Lubero и пише първото число - един - в средата на първата клетка на лентата на квадрат (или масив, ако щете):

// Създаване на магически квадрат невалидни генерира ()

// първия номер: номер = 1;

// първата колона за броя - средна стойност: колона = п / 2 + 1;

// низ за първия ден - първи: ред = 1;

// това въвеждане в квадрат: MQ [ред, COL] = брой;

Сега ние последователно паркиран до края на клетките - от две до п * н:

// придвижите към следващия брой: