Как да намерите областта на равностранен триъгълник основната формула

Изчисляването на площта на триъгълника в този случай ще се извършва в съответствие с формулата:

Лесно е да се измъкнем от този, който е известен с произволна форма, с три страни. Само във формулата трябва да се вземе предвид факта, че всички страни в триъгълника са равни.

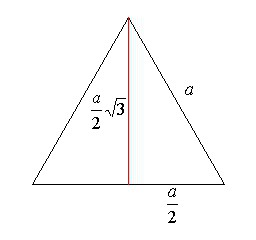
По-точно, необходимо чапла формула: S = √ (р (р-а) (р-Ь) (р-с)). Стойността за половината периметър на равностранен триъгълник е равна 3a / 2. По този начин, всяка скоба под корена се получи експресия ((3a / 2) - а). след това ще се преминава към / 2.

От трите скоби, а след това ще даде по-трета степен. Така че, това се превръща в 3/8.

Това все още трябва да бъде умножена по половината периметър, която се определя като сума от страните разделени от 2 до получаване на експресия: 3а 4/16. След като корен квадратен е само израз на воля, който е даден в първата формула за областта на равностранен триъгълник.

Ето защо не е необходимо да запомните много формули. Можете просто да се помни едно - Жирона. От него чрез прости математически преобразувания получава всички останали, например, равностранен триъгълник.

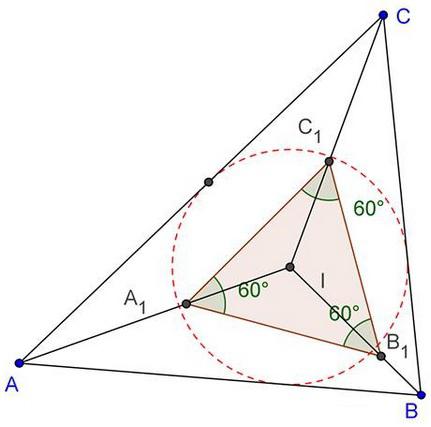
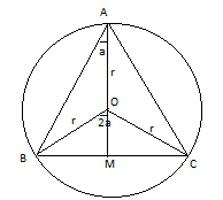
Формула 2: даден радиус на вписан кръг

Този израз е много подобен на предишния рекорд. Но има значителни разлики: използва различно писмо, ирационалността на нещо от знаменател, имаше един фактор на 3 и изчезна фигура 4. Като цяло, че е лесно да си спомня.

Тази формула е също така лесно да се измъкнем от това, което се дава за произволен триъгълник. Тя се умножава по сумата от радиуса на страните и се дели на 4. Тъй като страните имат еднаква стойност, като сумата се заменя със 3а. Сега трябва да се премахне "а" да има само една стойност радиус. Това ще изисква израз в която страна е разделена от продукта от 2 и синуса на ъгъла на противоположната страна. Тъй като ъгълът е 60 °, задължително стойност е √3 / 2. След това страните, изразени чрез радиуса, както следва: а = √3R. След проста трансформация може да дойде до експресията на квадрата, която се дава в началото.

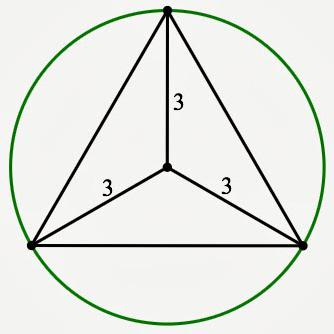
Формула 3: дадена окръжност кръг и радиусът

Той е много подобен на първия. Само в числителя се оказва под номер 3 и буквата променено на R.

Тъй като радиусът на два пъти това, което беше обсъден в предходния параграф, е ясно как се получава. Това просто въвеждане на R R / 2. И необходимите трансформации.

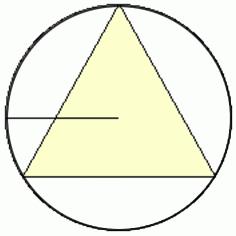
Следователно, формулата не мога да си спомня. Само имайте предвид съотношението на радиусите на вписаните и окръжности около равностранен триъгълник.

Формула 4: известна височина

В този случай, площта на равностранен триъгълник е равен на:

За да се разбере как е такава формула, отново, е необходимо да използваме обща за всички триъгълници. Тя изглежда като произведение на ръка на височината и ½. Сега, за да се намери областта на равностранен триъгълник, е необходимо да се припомни, или да оттегли математически израз за височината.

Нейната лесно да се учи, ако използваме факта, че височината на право форми триъгълник. Това означава, че височината може да се намери като крака - от питагорова теорема. Реваншът ще бъде равна на половината от страната, тъй като височината е и медианата (това е известно, собственост на равностранен триъгълник). Тогава височината се определя като корен квадратен от разликата на две квадратчета. Произход "а", а втората "а / 2". След ерекция остава във втората степен и корен екстракт: п = (√3 / 2) * на. От него с = 2N / √3. След като го замества в основната формула за всички триъгълници, които получаваме израз, който в началото на този раздел е в списъка.

Състояние. Изчислява областта на равностранен триъгълник, ако е известно, че неговата страна е 4 cm.

Решение. Тъй като знаем стойността на фигури страни, е необходимо да се използва първата формула.

Първо, трябва да квадрат номер 4. От това действие ще наброяват 16. Сега, това се свежда до Четворката, в знаменателя. И накрая в числителя е 4, а √3, а знаменателят е равен на една, което означава, че не може просто да пиша. Този резултат, който е трябвало да бъде намерена в проблема.

Отговор: 4√3 см 2.

Състояние. Всички страни на равностранен триъгълник са равни 2√2 дм. Изчислете своята област.

Решение. Аргументите са същите като в първия проблема. Само стойността на квадратен страна ще бъде различен. Необходимо е да се изгради отделно втория етап 2 и ирационалността. И резултатът е: 4 * 2 = 8. След редукция с знаменател е √3 и 2 в числителя и знаменателя изчезва.

Отговор: 2√3 дм 2.

Състояние. На равностранен триъгълник вписан кръг, радиусът на 2,5 см. Необходимо е да се изчислява площта на триъгълника.

Решение. За изчисляване на необходимостта желаната стойност да се използва втори формула.

Първо, трябва радиуса на квадрат. Вземи 6,25. След това тази стойност трябва да бъде умножена по 3. В резултат на това действие ще бъде броят 18.75. Но това не е окончателната стойност: тя ще бъде фактор √3, която присъства във формулата се използва.

Отговор: 18,75√3 см 2.

Състояние. Необходимо е да се определи какво е площта на равностранен триъгълник, ако знаем височината й - 3 дм.

Решение. Естествено, трябва да изберете четвъртата формула. С него най-лесният начин да намерите отговор на този проблем.

Човек трябва само да квадратен номер 3, който е на височината които да придадат стойност 9. След това го разделете на √3, стои във формулата.

Тъй като математиката не е прието да напусне ирационалността в знаменателя на отговора, тогава ще трябва да се отърве от него. За тази удар 9 / √3 необходимо да се умножава по фракция със същия числителя и знаменателя, а именно √3 / √3. От това действие се появява в стойността на числител 9√3, а знаменателят номер 3 ще се появи.

Тази фракция може да бъде и трябва да бъде намалена с 3. Това е крайният резултат.

Отговор: В района - 3√3 DM 2.

Състояние. Дан равностранен триъгълник, чиято площ е равна на 27 cm 2. От тази стойност, което трябва да знаете дължината на фигурата.

Решение. Тъй като това е страна, първата формула е подходяща. От него можете да незабавно да се извлече математически израз, който ще определи посоката на триъгълника.

За тази цел, мястото трябва да се умножава по четири и разделено на корен квадратен от три. Така че, за да получите стойността за партито на площада. За да получите точно посоката, в която трябва да се вземат корен. Изразът за частта ще бъде: а = 2 * √ (S / √3).

Тъй като районът е известен, че е възможно да започне веднага компютри. Радикалната израз прилича на частния 27 и √3. За да се отървете от ирационалност в знаменателя. Ще 27√3, разделен на 3. След намалението в знаменателя е 1, които не могат да пишат, а числителят е 9√3.

Следващата стъпка е да се извлече корен квадратен от получената експресията. Първият фактор дава стойността 3. Но вторият - √3 - се нуждае от внимание. За да се опрости задачата, можете да премахнете тези корени и заоблени ценности.

√3 = 1,73; Сега от него отново и да получите екстракт от корен 1.32.

Остава само да го умножете по 2 и да получите желания резултат.

Отговор: Страната е равен на 2,64 см.