Как да намерите най-вектор сумата

Добавянето на вектори на правилото за триъгълник. Нека а и б - две не нулев вектор. Отлагане вектор от точка О, и означават до края на буквата А. OA = а. Отлага от Вектор б, и означават до края на буквата Б. AB = б. Вектор, като се излиза в точка О и крайна точка Б (S = S) се нарича вектор сумата от а и Ь, и пише с = а + б. На вектор с каже, че е получен от комбинация от вектори а и б.

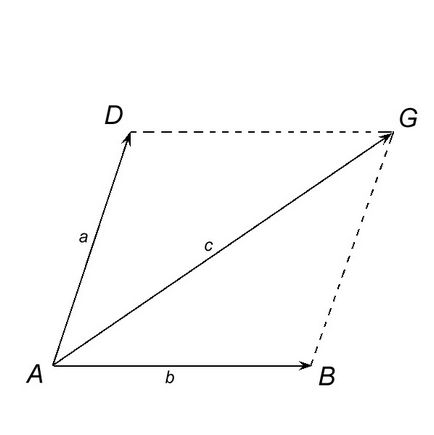
Сумата от две не-колинеарни вектори А и В могат да бъдат конструирани по правило, наречен правило успоредник. Отлагане точка А = В вектори AB и AD = а. След края на вектора и се направи линия, успоредна на вектор б, и до края на вектор Б - линия, паралелна направо на вектор. Нека C - точка на пресичане на изградените линии. Вектор AC = С - сума на вектори а и б.
с = а + б.

Вектор, векторът и обратното се нарича вектор, по - и така, че сумата от вектор и вектор S е равна на нула вектор:
а + (-а) = 0
Vector противоположна на вектора AB, наричана също BA:
AB = AA + VA = 0
Ненулева противоположни вектори имат еднакви дължини (| а | = | -а |) и в противоположни посоки.

сума вектор и вектор б противоположна на вектор разликата на две вектори, посочени като най - б, т.е. вектор + (Ь). Разликата от два вектора а и б означават - б.
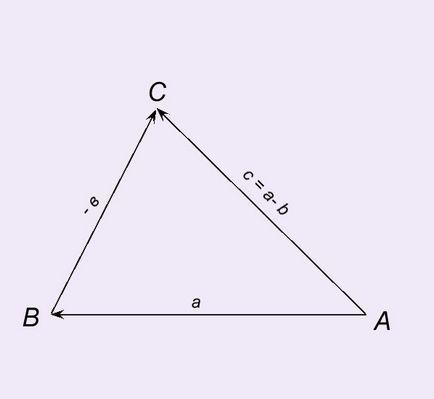
Разликата от два вектора А и В могат да бъдат получени, използвайки правило триъгълник. Отлагане точка А и вектора. AB = а. От края на вектора AB отложи вектор BC = -b, на вектор AC = C - разлика на векторите а и б.
с = а - б.

Имоти експлоатация на допълнение вектор:
1) нулев вектор имота:
0 = A + A;
2) добавяне асоциативност:
(А + В) + с = а + (б + в);
3) commutativity:
А + В = б + А;