Как да намерите на радиуса

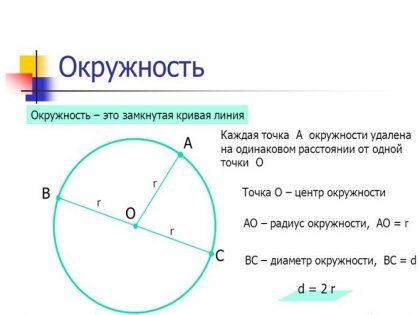
При доставка на различни изпити за студент се нуждае от основни познания по геометрия. Ето защо, всеки ученик трябва да знае как да се намери радиуса на кръга от неговата дължина, площ и други неизвестни по няколко начина, като се използва всеки в зависимост от някои или други известни данни.

Намиране на неизвестно радиус може да бъде чрез своите геометрични параметри: дължина, площ и т.н., а също и с помощта на известните три точки, които не се намират на една права линия, кръг, и са създали техните координати ...

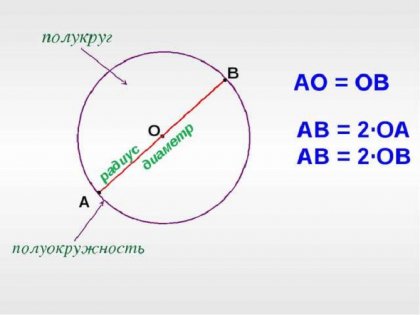
Както е известно, радиусът - е всяко разстояние от централната точка на точките, които са разположени директно върху кръга, чрез фигура център също посочена диаметър. Въз основа на две определяния, радиусът на кръга, за да се намери достатъчно само по следния метод.

Така, за да открие радиусът на кръга от известен диаметър, е необходимо да се прилага следната формула: R = D \ 2. В този израз г е неизвестен радиус (например, в см), и D - диаметър. В случая, когато диаметърът на кръга е броят 64, радиусът ще бъде равна на 32.

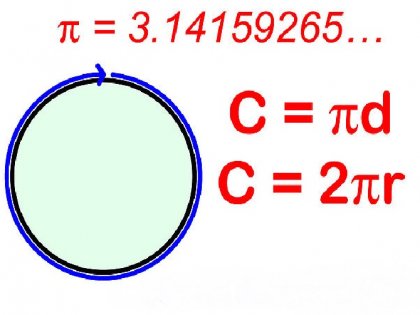
Намери кръг с радиус достатъчно лесно знам периферната дължина - т.е. дължината на всички негови съставни точки, разположени на еднакво разстояние от центъра на фигурата. За желаната стойност, е необходимо да се прилага следната формула: C = 2πr.

В тази формула С се приема за обиколка, π - константа е "Pi", която е равна на стойността 3,14, и R в училищни проблеми - желания радиус. Така, от тази формула експресиращи R, радиусът може да се намери, както следва: R = C \ 2π.

Очевидно е, че с по-голяма обиколка, на значително разстояние точки кръг с радиус по-голям.

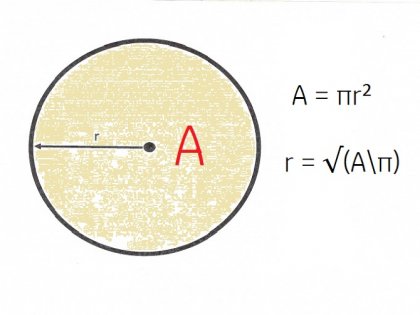
Ако проблемът е известен само в областта на кръг - това е, цялото пространство обхваната от окръжност, радиусът на окръжността може да се намери чрез следната формула: А = πr2.

Във формулата за зона А се приема обиколка, π - постоянна "пи", със стойност от 3.14, и г - желания радиус. От горната формула експресиращи желаната стойност, ние открихме, че радиусът може да бъде така: R = √ (А \ π).

По този начин, като се използва тази формула, известна площ 21 cm2 радиус на окръжността ще бъде 8.12 cm.

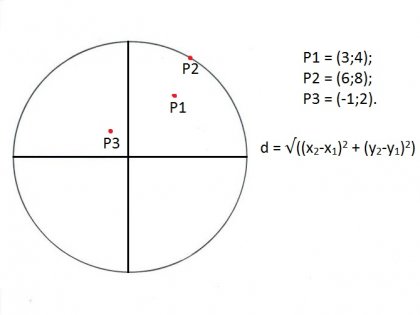
Има една теорема доказва, че през тези три точки, които не се намират в условията на една и съща линия, е възможно да се проведе само един кръг, така че можем да намерим радиуса на кръга, определена от три точки. И трите точки, трябва да имат техните координати.

Център допълнителен кръг, който може да бъде конструиран за по-голяма яснота, се изчислява споменатите три точки, както следва. По този начин, в центъра на фигурата е разположен вътре в триъгълник, неговите страни се изчисляват като се използва формулата: разстояние между две точки; на снимката тя е в списъка.

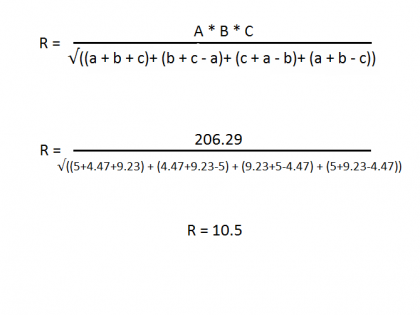
След са открити всички страни на триъгълника, е необходимо да се намери на радиуса на окръжност кръга, която се изчислява R = (ABC) / √ ((А + В + С) + (В + С - а) + (С + А - б) + ( A + B - в)), където а, в, с - тази страна на триъгълника, и г - желания радиус на окръжността.

По този начин, намери радиусът се свежда до правилното изчисляване на математически операции.

9621 9622 9623 9624 9625

За радиуса на кръга, за предпочитане:

- определи кои от представените в текста на методите са най-подходящи за ситуацията, описана в проблема;

- използване на последния метод, за да извърши действие, най-добре е последователно и без да бързат, защото рискът да се направи грешка тук е най-голям;

- боя ярки картини, съответните условия на проблема, т.е.. да. Понякога е добре да се направи добра работа при решаването на проблема (не само за намиране на неизвестен кръга).