Изпъкналостта, вдлъбнатина на графиката на функцията, инфлексната точка

характеристики на изследването в вдлъбнатината и изпъкналост може да бъде отделна задача, и един от етапите на пълно разследване на функцията и изграждането на своя график. Изпъкналостта и вдлъбнатина функция се появява само в определен интервал, и с които са свързани неща изброени дефиниции.

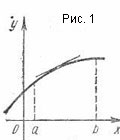
График диференцируема изпъкнала функция се нарича в интервал] а. б [, ако в този диапазон се намира под всеки от своята допирателна (фиг. 1).

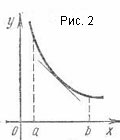
Графика вдлъбната диференцируема функция наречен в този диапазон се намира над всяка от допирателната (фиг. 2).

Теорема (достатъчно вдлъбнатина или изпъкналостите графики). Ако F функция (х) при всички точки в интервал] а. б [

крива Y = F на (х) е вдлъбната в този интервал; ако

при всички точки в интервал] а. б [, изпъкналата крива в този диапазон.

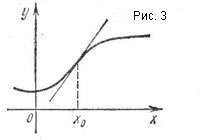
непрекъсната функция диаграма точка, в която се променя в вдлъбнатината или изпъкналост напротив, се нарича инфлексна точка.

От дефиницията следва, че едната страна на инфлексната точка на кривата се намира на допирателната, от друга страна - върху него, или обратно. Следователно, инфлексна точка на графика, за да покаже сегмент на допирателната в този момент пресича крива (фиг. 3).

Теорема (достатъчен показател за съществуването на инфлексна точка). Ако точката функция F на (х) е първата производна и втората производна в този момент е равно на нула или не съществува, и в допълнение, при преминаване през промени подпише

е инфлексна точка на графиката на у = е (х).

Така, за да се изследва естеството на изпъкналост на крива у = F (х). да намерите точките, в които или не съществуват, а след това, като се използват достатъчен критерий за разследване признаци на втората производна от ляво и от дясно на всяка възможна инфлексна точка (точно както е определено от екстремалната точка на първата производна).

Пример 1. Виж инфлексната точка и установи естеството на изпъкналост на функция графика.

Решение. Функцията е дефиниран за. И неговите производни. Намери възможните точки на инфлексия. Ако приемем, че ние се т. Е., Ако приемем, че ние получаваме.

Въпреки това, точките и не са включени в областта на дадена функция, така че може да има само една точка на огъване при. Ние разследваме знаците на втората производна около точката. Като точка гама, ние получаваме, тъй като приемането интервал точка има. Следователно, от ляво на кривата е изпъкнала. и от дясната - вдлъбнат. Ето защо, когато функцията график има точка на инфлексия.

Графиката на тази функция - Фиг. по-долу.

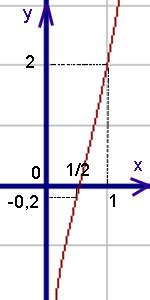
Пример 2. Намерете инфлексна точка, естеството на изпъкналост и вдлъбнатост и парцел функцията.

Решение. Функцията е дефиниран за. И неговите производни. Тук, както и в с и под. Следователно, от ляво на кривата е вдлъбната. и от дясната - изпъкнали. т.е. - на инфлексна точка на графиката.

Графиката на тази функция - Фиг. по-долу.

ПРИМЕР 3 Тест за функцията на изпъкналост, вдлъбнатина и инфлексна точка.

Решение. Намираме втората производна :. От уравнението получаваме една критична точка :. Проучване на знака в квартала се получи .. Вляво от точки (изпъкнали), както и правото - (вдлъбнатина), т.е., на точка е точката, интонация на функцията.

Графиката на тази функция - Фиг. по-долу.