Излага на функции

За да се разбере какъв е смисълът на екстремум на функция не е необходимо да се знае за наличието на първата и втората производна и да разберат тяхното физическо значение. Първо трябва да се разбере следното:

• екстремуми на функцията е увеличен, или, обратно, да се намали стойността на функцията в произволно малък квартал;
• в екстремум не трябва да е функция празнина.

И сега едно и също нещо, само на прост език. Погледнете върха на химикалка. Ако дръжката позиционира вертикално писмено край нагоре, а след това играта ще средна екстремум - най-високата точка. В този случай говорим за максимум. Сега, ако се превърне писането долния край, а след това топката ще бъде най-малко вече seredke функции. Използването на стойностите, посочени тук, изброени може да присъства за манипулация канцеларски молив. Така екстремуми на функцията - това винаги е критична точка: нейните върхове или дъна. В съседната част на диаграмата може да бъде произволно остър или гладка, но тя трябва да съществува в двете страни, но в този случай, точката е връх. Ако графиката е налице само от едната страна, на мястото на този екстремум няма да е, дори и ако от едната страна на екстремумът условия са изпълнени. Сега ще разгледаме крайностите на функции от научна гледна точка. Така че точката може да се счита екстремум, е необходимо и достатъчно, че:

• първата производна е равно на нула или не съществува в точката;
• първите деривативни промени подпишат в този момент.

Условия лекувани малко по-различен по отношение на производни на функция по-висок порядък, че е диференцируема в точката, е достатъчно да има производно нечетен ред, неравни на нула, въпреки факта, че всички производни на по-ниска за и трябва да има нула. Това е най-лесно тълкуване на теореми от учебниците по висша математика. Но е необходимо да се изясни този въпрос, като пример за обикновените хора. В основата е обикновен парабола. Самото начало на нулевата точка тя има минимум. Съвсем малко по математика:

• първата производна на (X 2) | = 2Х, 2Х за нулевата точка = 0;
• втората производна (2Х) | = 2, за нулевата точка 2 = 2.

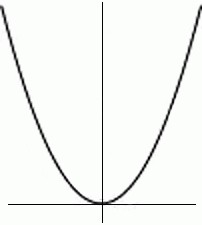
Такъв прост начин илюстрирано условия, определящи екстремум на функцията за първи ред и по-високи производни ред. Можете да добавите към това, че втората производна е точно много производна на нечетен ред, неравно до нула, което беше споменато по-горе просто. Когато става дума за крайностите на функция на две променливи, условията трябва да бъдат изпълнени за двете аргументи. Когато е обобщение, след това в хода са частични производни. Това е необходимо за съществуването на екстремум в точката на първите две производни са равни на нула, или най-малко един от тях не съществува. За задоволяване присъствие екстремум изследвана експресията представляващ продукт на разликата от втория ред и на квадрата на смесен втори ред производно функция. Ако този израз е по-голяма от нула, а след това до екстремум се случи, и ако има равен на нула, а след това остава открит въпросът, както и необходимостта да се проведат допълнителни изследвания.