Имотът на диагоналите на успоредник, най-големият портал за обучение

Имотът на диагоналите на успоредник

Теорема 6.2 (обратна теорема 6.1) .Diagonali успоредник пресичат и точката на пресичане са бисектни.

Доказателство. Нека ABCD - успоредника (Фигура 120.). Ще се проведе на диагонала BD. Имайте предвид, върху него около средата и на разширението на отсечката AB отложи сегмент ОС1. равен на AB.

От Теорема 6.1 АВС1 D четириъгълник е успоредник. Следователно пряк успоредно на BC1 АД. Но през точка В може да бъде извършена само една линия, успоредна на АД. Така че, прав BC1 съвпада с линията преди новата ера.

По същия начин, когато е установено, че линията DC1 съвпада с DC линия.

Следователно, точка С1 съвпада с точка С съвпада с успоредник ABCD АВС1 D. Следователно, неговите диагонали се пресичат и точката на пресичане са бисектни. Това доказва теоремата.

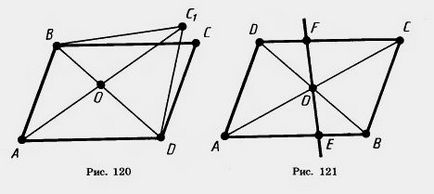
Проблем (6). Чрез диагоналите на успоредник пресечната точка на нещата. Докажете, че дължината на него, сключен между успоредните страни, е разделен на две от тази точка.

Решение. Нека ABCD - на успоредник EF - линия, пресичаща успоредните страни АВ и CD (фигура 121). Триъгълниците ОАЕ и ЕФЕ са вторият знак. Те раздават OA и OC са равни, тъй като G - среден диагонал AC. Ъглите в връх O са едновременно вертикално и ъглите на JAR и FCO са както вътрешни, така кръст лежи успоредно с AB, CD и разделят AC.

От равенството на триъгълници трябва да е равнопоставеност на страните: OE = НА, както се изисква.

А. В. Pogorelov, геометрия за класове 7-11, Учебник за учебни заведения