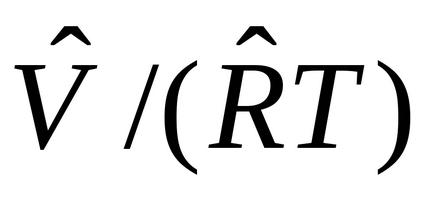Глава 2 от уравнението на състояние на материята

2.1. Топлинно-калорични уравнения на държавната

Общият брой на топлинна и термодинамични уравнения състояние на превозното средство се определя от броя на степени на свобода, т.е. включително въздействието върху превозното средство на обобщените сили. Тези уравнения са установени емпирично или е статистически методи за физика.

За прост TC (броят на степените на свобода, N = 2), която има един обобщен сила механични - davlenier. конюгат външен parametruV. взаимодействие с околната среда се характеризира само с едно външно параметър промяна в реакцията, (общи координира) - obemomV и temperaturoyT (независим параметър). След това състояние на равновесие на вътрешни параметри: налягане и вътрешни energiyuU може да се изрази като функционални зависимости: р = р (V, Т) - термичен уравнение на състоянието и U = U (V, Т) - калории уравнение на състоянието.

Термично състояние уравнение за прости TS могат да бъдат представени под формата на връзка: F (р, V, Т) = 0. Това уравнение е термодинамичните състояния на повърхността или повърхностите. За идеален газ уравнение на състоянието е термично Клапейрон уравнение: PV = МРТ. където R - специфичен постоянен газ.

Sostoyaniyaidealnogo уравнение калоричност газ може да се получи от Джаул закона: "Вътрешен sistemyU термодинамична енергия при Т = конст е независима от obemaV:

.

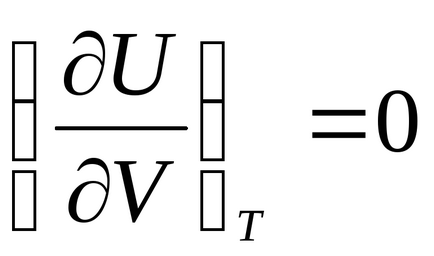
Разнообразяване на уравнение U = U (V, Т), ние получаваме:

,

където

- специфичната топлина на идеалния газ в protsesseV = конст (по дефиниция).

,

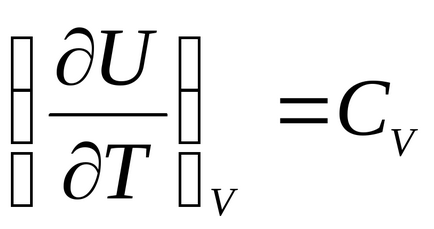
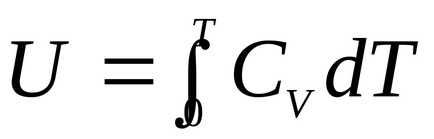
т.е. на вътрешната енергия на идеален газ е функция на температурата:

.

Калорична и топлинна уравнение на състоянието на идеален газ може да се получи от молекулно Kinetic Concepts.

2.2. Thermal уравнение на състоянието на идеален газ

Формално определя като слушането Клапейрон уравнение gazmozhno идеален газ:

.

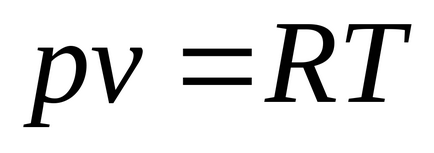
От физическа гледна точка на идеален газ - газ, чийто молекули лишен площта (обем на молекулите на газа в съда - Vmol<

,

където к = 1.380658 (12) 10 -23 [J / K] - Болцман константа;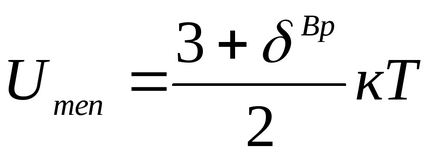

- правото на equipartition на енергия през степените на свобода на молекули.

Към 1 кг: PV = RT. където R, J / КГК - специфичен постоянен газ в зависимост от вида на газ, стр. Pa об. m 3 / кг; Т К.

За един мол от:

, където = 8.31441 J / Молко - моларен постоянен газ, еднакви за всички газове, ; M‧10 = -3. кг / мол - моларна маса, ; М 3 / мол - моларен обем, N мол - количество вещество.

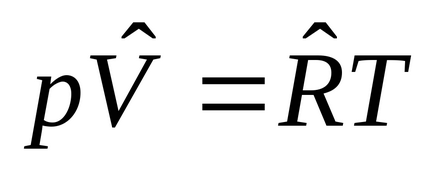
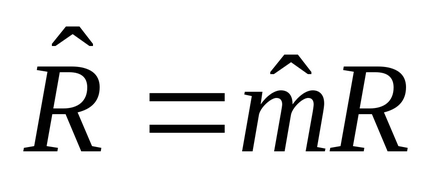
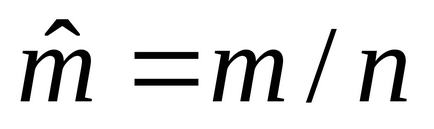
5. 1метър 3:

, където, кг / м 3. В тази форма, уравнението на състоянието се използва в аеродинамиката.

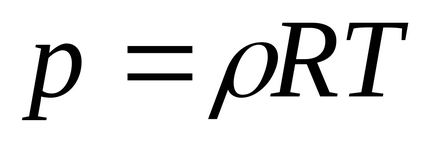
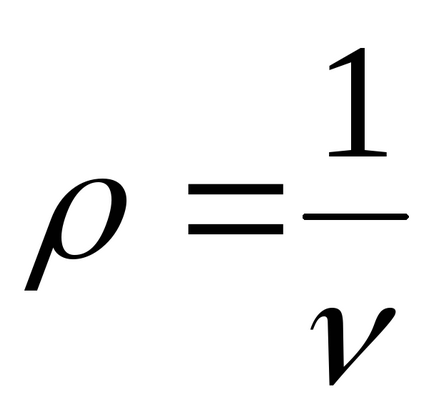
6. едно m 3:

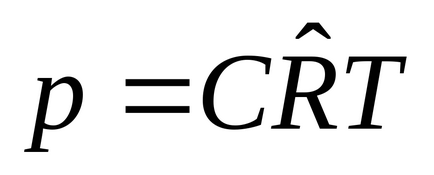
, където, мол / m 3 - моларна концентрация. В тази форма, уравнението на състоянието се използва в областта на химията.

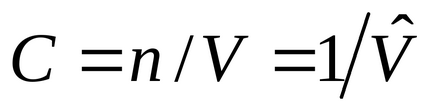
2.3. Термично състояние уравнение за реални газове

Специфичната форма на топлинна уравнение зависи от състоянието на агрегиране и вида на материала. Сега е добре развита уравнение на състоянието само реални газове. За уравнение на състоянието на кондензираната материя са изключително редки, тъй като те не са необходими за практически изчисления.

Форма на уравнението на състоянието на реални газове е силно зависи от размера на частиците и тяхната структура и естеството на взаимодействието между тях. Потенциалната енергия на взаимодействие Udvuh молекули зависи от разстоянието между центровете им -r. t.e.U = е (R). реални газове молекули имат краен размер и са привлечени един към друг със сила, която се увеличава с намаляване на средното разстояние между молекули, за разлика от идеален газ kotorogoU ш (R) = 0.

За изчисляване на потенциалната енергия U се използва предимно от Ленард-Jones:

.

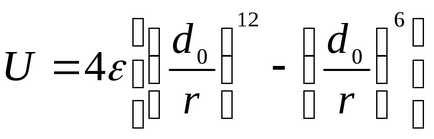
наименованията ценности

id0 е показано на фигурата, изобразяваща това zavisimostU = е (R).

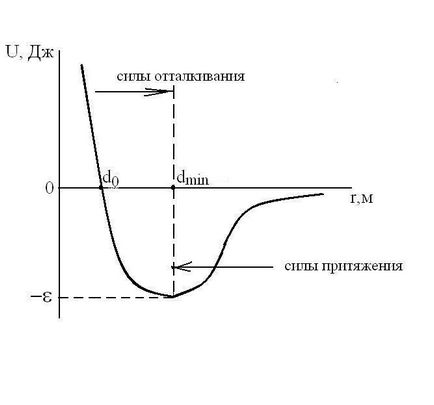
Взаимодействие между молекули сили

, [Н], много голям при малки разстояния между молекули (отблъскваща сила) и не позволяват да се намали количеството на газа е под определена граница (под rasstoyaniyar = Dmin). Този потенциал се отнася до групата на ван дер Ваалс (dalnedeystvuyuschih) сили. За голяма rasstoyaniyr potentsialU

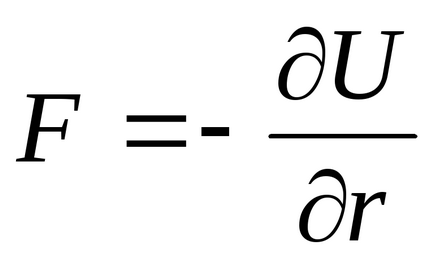
1 / R 6. сила и vzaimodeystviyaF

1 / R 7. За малки rasstoyaniyr (с енергични молекули подход) U

За сравнение, ние се отбележи, че за Кулон взаимодействието потенциал U

1 / R 2. Така, ван дер Ваалс сили намаляват с увеличаване rasstoyaniyar между частиците е много по-бързо от силата на Кулон. Затова държавната уравнение за реални газове обикновено не са подходящи за плазма. За плазмено състояние уравнение е получен отделно (Debye).

Взаимодействие сили в зависимост от разстоянието между частиците (F = F (R)) се използват за изчисляване на коефициентите в различни уравненията на състояние и действителната плазмен газ.

Най-простият състояние уравнението за реални газове е уравнението на ван дер Ваалс (1873) (В момента има повече от 150 емпирични уравнения). Това уравнение е от вида:

,

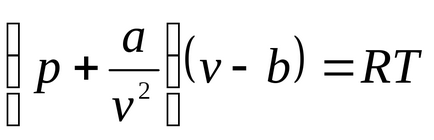
където б - корекция за молекулно обем, A / V 2 - коригиран за молекулно или вътрешно налягане определя чрез взаимното привличане на молекулите на газа. Konstantya и б зависят от вида на газ (от естеството на веществото).

За течности, това уравнение е силно в противоречие с експерименталните данни. Това уравнение показва възможното съществуване на два етапа и води до извода, че е налице критична точка. Ако атрибут параметри р, Т, V до критичната parametrampk, Тс, VK на критичната точка на фазовата диаграма и идентифициране

,,, ние получаваме намалява уравнение на Ван дер Ваалс:

,

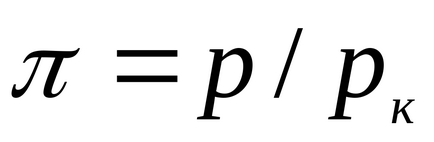
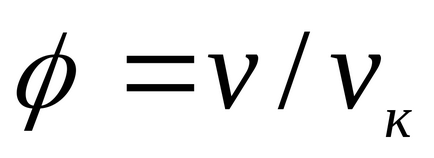
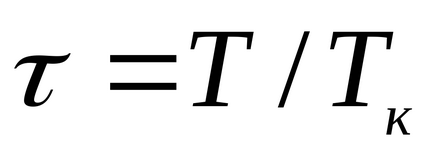
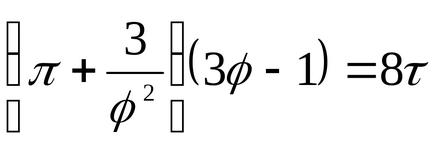
който изразява правото на съответните държави.

Съответните държави-членки, се наричат ​​с различни вещества, които имат едни и същи параметри, посочени

,. Вещества с подобна химична природа, които отговарят на това уравнение са термодинамично подобни ако техните критични фактори са едни и същи:

.

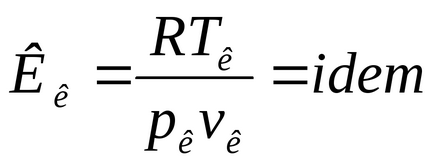
За vadervaalsovskogo газ Rk = 2.67.

Отклонение недвижими газ да свойства на идеален газ способността за пресоване може да се характеризира с величината на коефициента на свиваемост или

За идеален газ Z = 1. За недвижими gazaZ ≠ 1. Големината на коефициента на свиваемост зависи от налягането, температурата и вида на газ и може да бъде по-голяма или по-малка от единица, в зависимост от тези фактори.

Формулите на състояние могат да бъдат получени за реален газ, това взаимодействието на частиците. Тези уравнения се наричат ​​virial уравнението на състоянието, което от V - форма са както следва:

,

където А (Т) В (Т) C (T) - първи, втори и трети virial коефициенти, които зависят от температурата. virial уравнение на р-форма има формата:

Коефициентите А (Т) В (Т) C (Т), свързани с коефициенти А '(T), В' (T) C * (Т).

Първият коефициент (Т) се определя от двоични сблъсъци на частиците, вторият коефициент В (Т) - тройни сблъскване на частици и т.н. Едновременно сблъсък на голям брой частици - е малко вероятно. Най-важната роля, която играе двоични сблъсъци на частици. Ако сметката си от дясната страна на virial уравнения са запазени само две условия. Един пример за това уравнение е уравнението на ван дер Ваалс сили. коефициент на The (Т) се определя чрез интегриране на двоичен потенциал сблъсък. Колкото по-високо налягане, трябва да се разглежда на броя думи в дясната страна на уравнението virial толкова по-голям.

Термичното състояние уравнения за различните вещества също се определят от експерименталните данни за свиваемост Z = р

, за teploemkostiS = F (р, T) за температура ефект дроселиране. Следва да се има предвид, че използването на уравнението на състояние за идеалния газ дава приблизителни резултати, които са валидни за реални газове с ниска плътност, т.е. при ниско налягане и високи температури.