Фибоначи серия - един
произход
Последователността на Фибоначи е добре познат в древна Индия, където той е бил използван в метрични науки (прозодия, с други думи - прозодия), много преди тя става известна в Европа.
Проба дължина п може да бъде конструиран чрез добавяне на проба S п-1 в дължина. или дължина L на пробата п-2; и prosoditsisty показа, че броят на проби с дължина п е сумата от предходните две цифри в последователността. Доналд Кнут счита този смисъл в книгата "Изкуството на компютърното програмиране".
На Запад, тази последователност е проучен от Леонардо в Пиза, известен като Фибоначи, в работата си «Liber Абачи» (1202). Той смята, че развитието на една идеализирана (биологично нереалистично) заек население, като се предполага, че:
- В "нула" месец, има чифт зайци (0 нови двойки).
- В първия месец, на първата двойка ражда още един чифт (1 нов чифт).
- Във втория месец, двете двойки зайци имат други двойки и първата двойка от матрици (1 нова двойка).
- В третия месец, втората двойка и две нови двойки генерират общо три чифта стари и нови втора двойка от матрици (2 нови двойки).
Физически е фактът, че всяка двойка зайци произвежда още две двойки за цял живот, а след това умират.
Нека населението през последния месец н, ще бъде равна на F (н). По това време, само зайците, които са живели в МЕСЕЦ N-2 са способни на отглеждане и производство на потомство, а след това F (N-2) двойки ще бъдат добавени към сегашната популация на F (N-1). Така общия брой двойки е равна на F (п) = F (п - 1) + F (п - 2).
формула Бине му
Бине формула изразява изрично Fn стойност като функция на п:
,
където - златното сечение. В същото време, и са корените на квадратното уравнение.
От Binet формули следва, че за всички, има Fn-близкото цяло число. т.е.. По-специално, asymptotics.
И колкото по-обща формула:
- Числата на Фибоначи са представени на набор от ценности continuant единици: т.е.
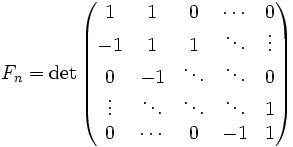
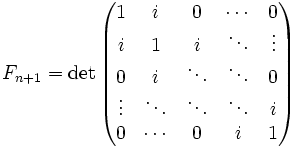
- Числата на Фибоначи могат да бъдат изразени по отношение на Chebyshev:
- За всеки п,
- Следствие. Изчисляване на детерминанти дава
- Най-голям общ делител на две числа е равно Фибоначи Фибоначи номер с индекса равна на най-голям общ делител на индексите м. Е. (Fm, Fn) = F (m, п). Последици:
- Fm е разделена от Fn ако и само ако m е разделена от N (с изключение на п = 2). По-специално, Fm е разделена от F3 = 2 (т.е., е дори) само за т = 3k; Fm е разделена от F4 = 3, m = само за 4k; Fm е разделена от F5 = 5 само за т = 5k и т. D.
- Fm може да бъде прост за прост m (с изключение единствено на m = 4) (например, броят 233 просто е, и индексът на 13, също е проста). Обратното не е вярно, първият Контрапример -. Не е известно дали наборът от числата на Фибоначи е безкрайна, е проста.
- Фибоначи последователност е частен случай на последователността замяна характерната полином х 2 - х - 1 и има корени.
- Връзки са подходящи фракции златен раздел φ и по-специално.
- Суми двучленни коефициенти на триъгълник на Паскал по диагоналите са Фибоначи оглед формула
- . 1964 J. Cohn (JHE Cohn) доказа, че само добра площади между Фибоначи номера са Фибоначи брой индекси 0, 1, 2, 12: F0 = 0 2 = 0. F1 = 1 2 = 1. F2 = 1 2 = 1. F12 = февруари 12 = 144. В този случай, за п = 0,1,12 вярно твърдение Fn = N2.
- Генериране функция на последователността Фибоначи е:
- Множество Фибоначи номера съвпада с набор от положителни стойности на полинома
Z (х, у) = 2xy 4 + 2 х у 3 - 2х 3 у 2y 5 - х 4 у + 2y,
на набор от числа х и у [2].
- Каталог и коефициент на всеки две различни Числата на Фибоначи различни от уреда, никога числото на Фибоначи.
- Последните номера Фибоначи образуват периодична последователност с период 60, последната двойка Фибоначи номера образуват последователност на периода 300, последните три цифри - с периода 1500, последните четири - с периода 15000, последните пет - с периода на 150000 и др ...
Вариации и обобщения
- номера tribonachchi
- Числата на Фибоначи са специален случай на Лукас последователности, както и техните допълнения са Лукас номера.
В други области
Вижте какво "на Фибоначи поредицата" в други речници:
Фибоначи номер - няколко фракции, при което всяка следваща фракция, получена чрез сумиране на числителите и знаменателите на предишните две фракции. Той се използва за характеризиране на phyllotaxis в растенията ... Анатомия и морфология на растенията
Фибоначи - Леонардо Pizansky Леонардо Пизано Роден ок. 1170 ... Wikipedia
Фибоначи номера - Фибоначи елементи числени последователност 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946 ... (последователност A000045 в OEIS), в която всеки следващ брой е сумата от двете ... ... Wikipedia
Фибоначи код - Фибоначи кодиране смесени радикали числа въз основа на номера на Фибоначи F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, и т.н. Запис номер в Код 0 на Фибоначи FSS ...... 0 0 F2 = 1 1 ... Wikipedia
Фибоначи кодиране - Фибоначи кодиране смесени радикали числа базирани на Фибоначи номера F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, и т.н. Запис номер в Код 0 на Фибоначи FSS ...... 0 0 F2 = 1 1 ... Wikipedia
Фибоначи последователност - последователността Фибоначи, математическа последователност, която всеки член е сумата от предишните две. Така, ако тото срока на последователност е означена хп, тогава цялата последователност е справедливо уравнението ... ... Наука и Технология енциклопедичен речник
Кодиране на информация - създаване на кореспонденцията между елементите на съобщението и сигнали, като се използва, на които могат да бъдат фиксирани тези елементи. Б. Да множество съобщения, както и азбуката със символите. Да предположим, че краен последователност от символи, наречен. дума, ... ... Физическо енциклопедия
История на аритметика - аритметика. Pinturicchio боядисани. Борджия апартаменти. 1492 1495. Рим, Ватикана дворци ... Уикипедия
- Веке. Alive Crystal. Златни раздел Matrix. Тази книга се фокусира върху многомерен човешки и трите основни етапи на Ерата на Водолея: Трансформация, хармонизация и преходите. Ако говорим за многоизмерност, рано или късно, нашите изследвания ... Прочетете още Купи за 549 рубли
- Живо кристал. Golden раздел Matrix. Тази книга се фокусира върху многомерен човешки и трите основни етапи на Ерата на Водолея: Трансформация, хармонизиране и преходите. Ако говорим за многоизмерност, рано или късно, нашите изследвания ... Прочетете още Купи за 549 рубли
- Разберете в 30 секунди. Математика за 30 секунди. Браун, последната теорема на П. Ферма, числото "пи", поредицата на Фибоначи, триъгълник на Паскал. Разбира се, вие сте наясно с какво се разбира под тези понятия, или са чували за тях. Но ако можете да завладее всички гости на партито, ... Прочети повече Купи за 496 рубли