Анализ на статично неопределими греди 1

Примери за разтвори на проблеми за якост на материалите

Тази страница е пример за решаване на проблема от силата на материали, което е необходимо, за да се изчислят статично неопределими греди, натоварени напречни фактори сили. Изчисленията са дефинирани линейно движение на секциите на напречни греди по нейната дължина.

Изчислените резултати са украсени греди огъващ момент диаграма и силите на срязване и линейно движение.

Студентите от техническите специалности на висшите учебни заведения като методическа помощ, предлагани за изтегляне готови варианти на контролни работи по силата на материали (приложна механика). Представени примери на техните задачи и решения, предназначени специално за студентите от Техническия университет-членка на Алтай.
Опции контролират творби могат да бъдат изтеглени в Word формат, за да направи преглед на процедурата по задачи решение или за печат и защита (съвпадението на опции).

Анализ на статично неопределен лъч

Състояние на проблема:

В статично неопределен лъч с два крака, твърди глави А и осово-подвижния супорт Б. въздейства от външни сили: на F сила и разпределен товар Q (виж фигура 1 ..).

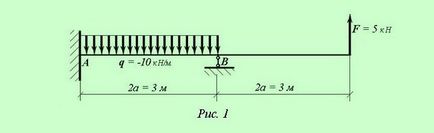
изисква:

Определя реакциите на подкрепа, изграждане на диаграми на срязващи сили, огъващи моменти и линейно движение.

Предистория:

• странична сила F = 5 кН;
• разпределен товар р = -10 кН / m;
• линеен стойност = 1.5 m

• първоначалното координиране разпределен товар ZQ = 0;
• разпределен товар приключва координира ZQ = 2 а;
• ZF = 4 - координира прилагането на концентриран сила;
• ZB = 2 - Подкрепата координира.

Начертайте схема за лъч в съответствие с първоначалните данни.
Anchorage разположен на левия край на гредата, в същото изберете произхода.

Този лъч е статично неопределен веднъж, защото реакциите поддържащите го има повече от уравнения на статиката единица. Следователно, използването на статични методи, за да се определят неизвестните фактори сила е невъзможно, като реакция на подкрепа е "екстра" и неизвестни фактори сила е един по-големи от равновесни уравнения.

За да се реши проблемът с използване на метода Верешчагин, отхвърляйки "екстра" на връзката и да го замени с неизвестна сила X1. За допълнителна връзка може да приеме всички допълнителни реакции с изключение на надлъжно действа HA реакция. защото без него, лъчът няма да може да се поддържа баланс.

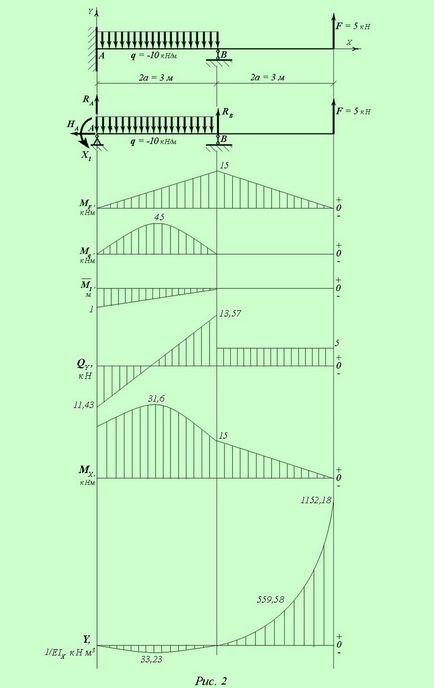
Ние приемаме за допълнителна връзка реактивен въртящ момент УО на. композира лъч еквивалентна верига (Фигура 2), и напиши каноничен сила метод уравнение веднъж статично неопределен система:

Като допълнителна връзка, ние изхвърля реактивния въртящ момент даден каноничен уравнение е ъгълът на въртене на гредата в произход т. Е. В закрепване.

За изчисляване на коефициентите на каноничната уравнението конструират товари MF (от външни натоварвания и F р) и единица M1 (от усилията X1 = 1) огъващ момент, и след това да ги размножават в съответствие с метода, Верешчагин (вж. Фиг. 2).

Като Верешчагин продукт диаграми MF × M1 е равна на площта на диаграми товарни умножено по височината на схемите за единица продукция, предприети в рамките на центъра на тежестта на диаграми карго. По този начин двете диаграми не трябва да имат точките фрактури, и най-малко една от схемите да бъде линейна.
За удобство на изчисления листовиден диаграми MF и MQ. изграждането им на отделни класации.

Според схемата на Фигура 2 коефициенти на каноничните уравнения са дефинирани чрез формулите:

Ние замести стойностите, получени в каноничното уравнение и да намерите неизвестен сила X1:

Статично неопределеност описано.
отрицателно X1 на стойност сила показва, че посоката на тази сила е разположен първоначално фалшива, и в действителност това е насочено към противоположната страна, т.е. огъващият момент действат в плътно запечатване на MA = - .. X1.

Сега, от уравненията на статиката намерят опорни реакции на лъча:

Положителната стойност на получената реакционна RB показва, че посоката на диаграмата на Фигура 1 е избран правилно.

Тъй като реакцията е положителен, посоката на схемата е избран правилно.
За проверка на резултатите, получени форма на уравнението на равновесие на силите, действащи върху гредата:

За конструиране на диаграма линейно изместване Y (отклонение) е необходимо да се определят стойностите на 4 ... 5 части от светлина.
В нашия случай, известно е, че движението на опорите А и В са равни на нула, т.е.. Е. YA = 0 и Yb = 0.
Ние изчисляваме огъването в средата на многочленни греди координира z1 = а. Z2 = 3 и в крайната част на гредата, където силата, приложена F (z3 = 4 а).
Уравнения отклонения в тези участъци имат формата на първоначалните параметри на метода:

Според получените приблизителните данни, изграждане на диаграми на странично QY сили. огъващи моменти MX и умира Y (вж. фиг. 2).