3 проекция вектор от вектор

Скаларни квадрат на вектора

И какво ще се случи, ако векторът се умножава по себе си? Ясно е, че векторът е една и съща посока с самият poetomuili

Броят се нарича скаларна квадрата на вектор, и се определя като

По този начин, скаларна квадрата на вектора е квадрата на дължината на вектора: От това уравнение може да се получи дължина на вектор формула:

Ъгълът между векторите

Отново, погледнете нашата формула .po правило на част и дължината на скаларен продукт на вектори - брой. Така че, също е число. Ако е известен косинус на ъгъла: след това с помощта на обратна функция лесно да се намери ъгъл :.

Проекция на вектор. Проекцията на вектора на координатните osi.Napravlyayuschie уюта на вектора

Помислете векторите:

Ако остър ъгъл между векторите (както е показано), след това

Ако vektoryortogonalny. след това (проекцията на точка, се считат за размерите на който да бъде нула).

Ако тъп ъгъл между векторите (на фигурата психически позицията стрелка вектор), след това (със същата дължина, но се приема със знак минус).

Отлагане тези вектори от една точка:

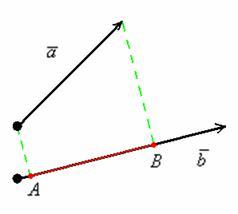
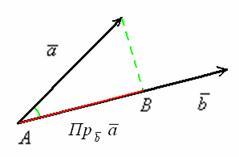
Очевидно е, че когато се движите, че не променя вектора на проекцията

Помислете за един правоъгълен триъгълник. Косинус на малък ъгъл е съотношението на съседната част на крака на хипотенузата. В този случай:

От друга страна, вече получени формулата на косинуса на ъгъла между векторите:

По този начин: Или