Преходът към нова база

Poort в R има две основи: стари EL. e2. ен и нова електронна л *. e2 *. ен *. Всяка нова база вектор може да бъде представена като линейна комбинация от базисни вектори на стария:

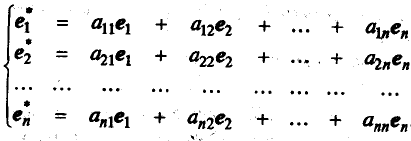
Преходът от старата към новата база, можете да зададете на матрицата преход

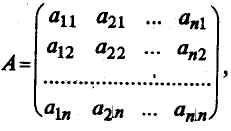
Имайте предвид, че коефициентите за умножение на новите базисни вектори на старите основна форма колони вместо редове на тази матрица.

Носител - неособена матрица, тъй като в противен случай колони (и следователно базисни векторите) за линейно зависими. Следователно, има обратна матрица А -1.

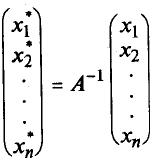
Заместник в това уравнение ел * стойности. e2 *. ен * от предишната система:

С оглед на линейна независимост на векторите ел. e2. ен всичките им коефициенти в последното уравнение трябва да са нула. Следователно:

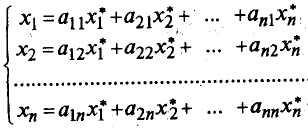
или под формата на матрица

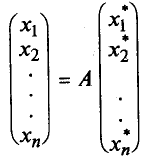
Увеличаването двете страни с -1. получаваме:

Например, да предположим, че в основата ел. e2. e3 даден вектор а1 = (1, 1, 0), а2 = (1, 1, 1), а3 = (-3, 5, -6) и Ь = (4, -4, 5). Покажете, че векторите др. А2. a3 също образуват основа, и да се изрази в тази основа vektorb.

Ние показваме, че вектор Ал. А2. a3 са линейно независими. За да направите това, ние се увери, че в ранг на матрица, съставена от тях е три:

Имайте предвид, че първоначалната матрица е нищо друго освен преход матрица А. Всъщност, връзката между базите EL. e2. e3 и др. А2. A3 може да се изрази в системата:

+ 6 = 0 - 3, - 0 - 5 6 + 4 =

линейни оператори

Линеен оператор (трансформация картографиране) п двумерен вектор пространство наречен praviloY = F (X), с което всеки вектор X е назначен уникален vektorY, където се съхраняват линейни операции на вектори, т.е. притежава свойствата на мястото:

1) е (X + Z) = F (X) + F (Z) - адитивност собственост на оператора;

2) е (X) = f (X) - еднаквост собственост на оператора.

Човек може да се докаже, че всеки линеен оператор отговаря на квадратна матрица в тази база. Обратното също е вярно: Матрица всички п-ти за линеен оператор отговаря на п-тримерно пространство.

Следователно, линейна трансформация може да бъде определено по друг начин: линеен оператор п двумерен вектор пространство, зададени на квадратна матрица А се нарича трансформира, че всеки vektoruX записва под формата на матрица колона, асоциирани с вектор (X) = A * X =.

Матрица се нарича матрица на оператора в тази основа и ранга на тази матрица е с ранг на оператора.

Например, ако е даден оператор линейна матрица, след otobrazhenieYvektoraX = (4, 3, 1) ще бъде равна на

.

Имайте предвид, че единичната матрица, уточнява трансформацията на идентичността (операторът на идентичност), тъй като се умножава с вектор, получаваме същия вектор.

А нула матрица се определя като нула оператор. присвоява всички вектори на пространството във вектора нула.

Лесно е да се уверите, че диагоналната матрица, диагонал, който е на стойност един и същ номер, операторът определя размножаването на вектора от този номер.

Теорема. Матрицата A и A * на една и съща линия в основата ел. e2. и ен ел *. e2 *. ен * са свързани с А = C -1 * AC, където С - матрица на преход от стария към новия основа.

Доказателство. Означаваме Yotobrazhenie vektoraXv baziseel. e2. ен. и същ вектор в основата ел *. e2 *. ен * означават Х * и Y *. Тъй като C - преход матрица, ние можем да напишете:

Ние се размножават както в лявата част на първото уравнение от матрицата:

Тъй AX = Y, poluchimY = ACX *. т.е. Су * = * ACX. Увеличаването двете страни на това уравнение от -1. получаваме:

C -1 Су * = C -1 * ACX

Тъй Y * = A * X *. А = C -1 * АС, както се изисква.

Например, да предположим, че в основата ел. e2 матрица от =. Намерете матрицата на този оператор в основата ел * = ел -2e2. Е2 * = 2дл + е2.

За това ние изграждане на преход матрица C = и обратен матрица C -1 |. С | = 5 ,,. след това